 |
Select the correct answer and then click
Continue. |
|
A cylinder has a volume of 320 cubic cm and a
radius of 4 cm. What is the greatest number of spheres of radius
3.5 cm that the cylinder can hold?
|
The number of spheres that will fit into the
cylinder is dependent on the height and width of the cylinder relative
to the spheres. Since we have the volume and the radius (half of the total
width) of the cylinder, we can determine the height of the cylinder as
well:
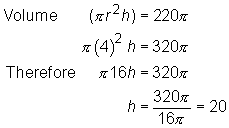
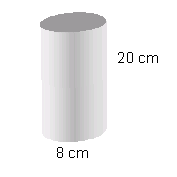
Our cylinder has a height of 20 cm. Its diameter
is equivalent to twice its radius: 2 
4 = 8 cm:
The spheres have a radius of 3.5 cm, or a diameter
of 7 cm. Therefore, each sphere measures 7 cm at its longest cross section,
and 7 cm at its widest cross section:
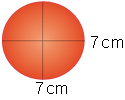
Since each sphere is 7 cm across and the cylinder
is only 8 cm wide, the spheres can only fit on top of one another within
the cylinder; they cannot be next to each other because the cylinder isn't
wide enough. The sphere is also 7 cm in height. The height of the cylinder
is 20 cm, so we can fit 2 spheres on top of one another within the cylinder:
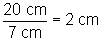, remainder of 6 cm.
Choice (B) is correct.
Back Next
Next to display next topic in the chapter.
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.