|
This problem must be solved algebraically, so English
to algebra translation skills will come in handy. We can begin by setting
up our equation:
| 3x divided by 6: |
 |
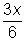| is: |
 |
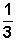less than: |
 |
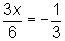| the reciprocal of 2y: |
 |
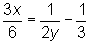Now we can simplify our equation and solve for
x and y, or, if we're lucky, for  :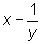
On algebraic equations, it's sometimes necessary
to solve for one variable (i.e. x), and then use that value to
find the other (i.e. y). This was not the case this time; the equation
simplified to the complicated term for which we were searching. If the
one-variable, two-variable approach were the only way to handle this problem,
it would be a time-consuming question. On complicated equations, always
keep in mind what you must find to answer the question, and try to rework
your equation to fit it. There is often a key step that will reveal the
problem and get you through the question quickly.
|