
This question asks us to find the ratio of the
area of the circle to the area of the polygon. To do so, we will need
to determine the radius of the circle. We will also need to figure out
a way to determine the area of the polygon; since polygons are composed
of more familiar figures such as triangles and quadrilaterals, a good
approach will be to break up the polygon into these more manageable shapes.
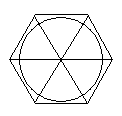
Now, what are we given? We are told that the
circle is inscribed in the polygon. Therefore, we know that 1) the sides
of the polygon must be equal  ,
2) the line segments that join opposite angles of the polygon are equal
in length, and they also intersect at the circle's center, and 3) the
circle's radii form right angles with the polygon sides at the point of
tangency.
,
2) the line segments that join opposite angles of the polygon are equal
in length, and they also intersect at the circle's center, and 3) the
circle's radii form right angles with the polygon sides at the point of
tangency.
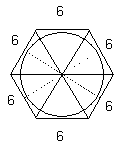
Therefore, we have a polygon composed of 6 equilateral
triangles; because the outer leg of each triangle is 6, the angles that
converge at center of circle must also be equal  .
The two other angles in each triangle must also be equal since their opposite
sides are equal
.
The two other angles in each triangle must also be equal since their opposite
sides are equal 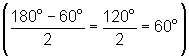 .
.
Our 6 equilateral triangles can be further broken
down into 12 30°/60°/90° triangles formed by the circle radii.
Now, since we have the length of one side of a 30°/60°/90°
triangle  we can determine the
radius of the circle by using ratio lengths of a 30:60:90 triangle. Once
we have radius we can use it to find area of each triangle, and then sum
them to get the area of the polygon.
we can determine the
radius of the circle by using ratio lengths of a 30:60:90 triangle. Once
we have radius we can use it to find area of each triangle, and then sum
them to get the area of the polygon.
Circle Radius & Area:
A 30°/60°/90° triangle has side lengths in the ratio of  .
If the shortest side of this type of triangle is 3, then the second longest
side must be
.
If the shortest side of this type of triangle is 3, then the second longest
side must be  . Therefore, the
circle's radius measures
. Therefore, the
circle's radius measures  , and
the circle's area is
, and
the circle's area is
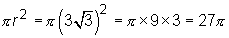 .
.
Polygon Area:
If the circle's radius is  ,
then the area of each 30°/60°/90° triangle is
,
then the area of each 30°/60°/90° triangle is 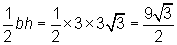 .
The polygon is composed of 12 30/60/90 triangles, so the polygon area
is
.
The polygon is composed of 12 30/60/90 triangles, so the polygon area
is 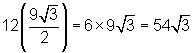 .
.
The ratio of the area of the circle to the area
of the polygon is 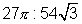 , or
, or 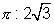 .
.
Back Next
Next to display next topic in the chapter.
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.