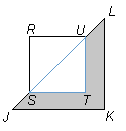
|
In the figure above, RSTU is a square
with an area of 8 and JKL is an isosceles triangle.
If JS = UL = 2, then what is the
perimeter of the shaded figure?
|
 |
Consider your answers to the following
questions, and then click Continue. |
- What is the question asking us to find?
- What information has it provided to
us?
- What shared feature will get us to
the correct answer?
|
|
Use the information provided in the
question stem to determine the following measurements. Enter your
responses in the boxes below, and then click Continue. |
|
What is the length of side ST ?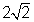
What is the length of side TU ?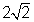
|
|
What is the length of side JK ?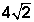
What is the length of side KL ?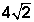
|
Triangle STU is half a square; half squares
are isosceles triangles with side lengths in the ratio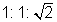 
.
Since the legs of STU are also sides of RSTU, they must
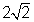measure . The lengths of the
sides of STU are therefore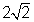
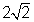: : 4.
We are told that JKL is also an isosceles
triangle. We can determine the length of its hypotenuse JL by adding
the lengths of JS, SU, and UL. We are told in the
stem that JS and UL are both 2, and we have just determined
that SU, the hypotenuse of the isosceles triangle STU, is
4. Therefore, the length of JL is: 2 + 4 + 2 = 8.
Now that we know the length of the hypotenuse
of the larger isosceles triangle, we can determine its legs. There are
two ways we can find these measurements:
1) Triangle to Triangle Ratio Triangles STU
and JKL are both isosceles triangles, so their legs should be in
the same ratio — .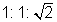
We have all measurements for the smaller triangle, but need to find out
the legs of the larger. We can set up a ratio to get this information:
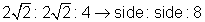. Since the hypotenuse of the
larger triangle is twice the length of the smaller triangle's hypotenuse,
then the legs of the larger triangle should be twice the length of the
legs of the smaller triangle: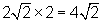 
.
Each leg of the larger triangle measures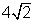 
.
2) The Pythagorean theorem. Since JKL
is an isosceles triangle with a hypotenuse of 8, we can use the Pythagorean
theorem to figure out the lengths of the legs:
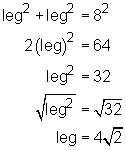
Back Next
Next to display next topic in the chapter.
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.