Choice (B), 32, is not the correct
answer. The question stem states that MN is half the length of JK.
According to our sketch, this is not the case when KM = 32. When
KM = 32, MN is too large in comparison 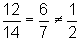to JK:  .
We need a larger number for KM so that MN becomes smaller relative to JK.
At this point, we can select Choice (A), 40,
as the correct answer without even Backsolving
it. Why? Two reasons: 1) It's the only larger answer choice left,
and 2) we can eliminate Choice (E), "It cannot be determined…"
We know that this question CAN be solved since we just evaluated answer
Choice (B) and were able to get a concrete, though incorrect, value.
Remember, however, that this problem may also
be solved algebraically, The algebraic
solution is quite fast; if you were able to translate the relative
segment lengths into their algebraic equivalents, the solution to this
question would be pretty quick. So even though Backsolving works well
here and on many other problems, it is well worth your time to practice
translating wordy algebraic problems to their mathematical equivalents.
|