How to Find the Measure of an Inscribed Angle

How to Find the Measure of an Inscribed Angle

Finding the measure of an inscribed angle requires knowing a little information. In this lesson, we'll find the measure of an inscribed angle when we know the measure of the central angle or one or more of the arcs formed by the angle.

Circles

Circles. They're everywhere. And they're so pretty and perfect and, well, round. Oh, man, look what happened:

The lines in the circle are called chords.

Someone drew lines on our nice clean circle. Well, let's take these graffiti lemons and make geometric lemonade, so to speak.

Inscribed Angles

We call these lines chords. These aren't the chords you need to play the guitar. In geometry, a chord is just a line with endpoints on our curve.

When we have two chords that share an endpoint, we get an angle. That angle is called an inscribed angle. We can officially define this as the angle formed by points on the circle's circumference. In this angle below, which we call angle ACB, point C is the vertex, and points A and B are the endpoints.

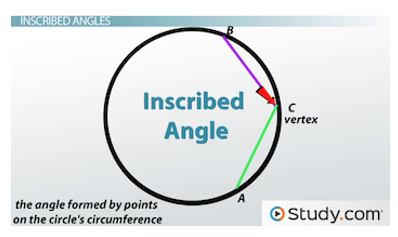
C is the vertex, and points A and B are the endpoints in this inscribed angle.

Using Central Angles

There are two ways to determine the measure of inscribed angles. First, the measure of an inscribed angle is half the measure of the central angle with shared endpoints. The central angle is like the inscribed angle, but instead of chords with endpoints on the circumference, it is made of radius lines that meet at the circle's center.

You can kind of see below how the chords forming the inscribed angle seem to go about twice as far as the radius lines of the central angle, so that makes sense, right? This means that if you know the measure of the central angle, just cut it in half, and you have your inscribed angle.

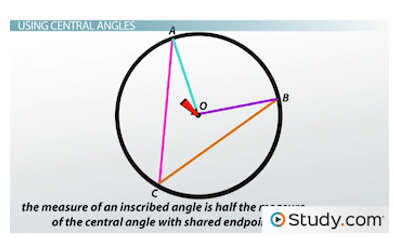
You can use the central angle to find the measure of an inscribed angle.

This is pretty straightforward, so we're not going to dwell on it. But if you ever see a question like this - 'If central angle AOB measures 80 degrees, what is the measure of inscribed angle ACB?' - know that you just need to cut that 80 in half. So, it's 40 degrees.

Using Arc Lengths

The second method for finding the measure of an inscribed angle is a bit more challenging. We can move point C around like a tilt-a-whirl, and the measure of the angle is unchanged. That means that if we have two inscribed angles that share endpoints, they will be congruent. Why is that true? Because the angle's measure isn't dependent on the location of the vertex, only on the endpoints.

Now, when the chords of our angle hit the circumference at points A and B, they form an arc. That's arc AB:

Arc AB

And the measure of an inscribed angle is half the measure of the arc it intercepts.

I'm a visual person, so I like to make sense of this by looking at an angle. See here?

Angle ACB is 45 degrees.

This inscribed angle has one chord that's a diameter of the circle. The other chord hits the circle just above the center. So, arc AB is one quarter of the circle. How many total degrees are there in a circle? 360. And what's one quarter of 360? 90. So, arc AB is 90 degrees. And as you can see, angle ACB is 45 degrees, or one half of 90.

This also works if we draw two chords out like below to form a right angle.

These endpoints form an arc that is half of the circle.

Notice where those endpoints are. They form an arc that's half of the circle, or 180 degrees. 180 divided by 2? 90!

Finding the Arc Measure

If you get asked to find the measure of an inscribed angle and you're given the measure of the arc it intercepts, you're all set. Just divide by 2. But what if it's a little more complicated?

Look at this one:

Angle ACB is 50 degrees.

We want to find angle ACB. But all we know is that arc AC is 120 degrees and arc BC is 140 degrees. But wait - we know the sum of all the arcs is 360. So, arc AB is 360 minus 140 and 120. That means arc AB is 100 degrees. And then angle ACB is just half that, or 50 degrees.

What about this one?

Angle ACB is 22 degrees.

This time, we're just given arc BC, which is 136 degrees. What about AC? Well, hold on. We don't need it. Note that chord AC goes through the center of the circle. This means that the sum of arcs AB and BC is 180. So, if BC is 136, then AB is 180 minus 136, or 44. That means angle ACB is half of 44, or 22 degrees.

Lesson Summary

Inscribed angles are formed by two chords that share an endpoint, known as a vertex. If we know the measure of the central angle with shared endpoints, then the inscribed angle is just half of that angle. If we know the measure of the arc our inscribed angle intercepts, we just divide that in half to get the measure of the inscribed angle. If we aren't given the intercepted arc length, but we know the lengths of the other arcs, we can determine the intercepted arc length with the knowledge that a circle has a total of 360 degrees, while a semicircle has a total of 180 degrees.