Finding the Properties of Three-Dimensional Objects on the SAT

Finding the Properties of Three-Dimensional Objects on the SAT

Struggling with 3-D geometry problems on the SAT, like the problems about cubes and spheres? In this lesson, you'll learn how to crack them by breaking them down into more familiar 2-D shapes and solving from there.

3-D Shapes

Unlike 2-D geometry, three-dimensional geometry, or 3-D geometry, deals with objects that have three measurable dimensions: length, width, and height. You can see this if you compare a 2-D shape, like a square, to its 3-D equivalent, a cube. The square has only length and width, but the cube has length, width, and height. The biggest trick to mastering 3-D geometry on the SAT is to realize that most of it really isn't about 3-D shapes at all. Instead, it's about collections of 2-D shapes that just so happen to be arranged into something we recognize as a cube or a sphere.

You could see this shape below as a cube, but you could also see it as six squares stuck together, and that's a lot easier to work with.

Thinking of this cube as being six squares stuck together makes it easier to work with.

When you're working with 3-D shapes, this ability to break them down into their component 2-D parts will give you a big boost on the test. In this lesson, we'll cover one of the most important 2-D breakdown shapes: hidden triangles. Then, we'll walk through a basic example and a second example with a cylinder to show how triangles can even help with rounded shapes if you know how to use them.

Hidden Triangles

Hidden triangles are one of the biggest 3-D tricks on the SAT. These are most commonly right triangles but can sometimes be other types of triangles as well. Just to show you how this works, take a look at some of the triangles lurking inside just one cube. Here's one that you could use to find the distance between points A and B, or the diagonal, of one side of the cube.

Here's another that you could use to find the distance between points C and D, drawing a line right through the center of the cube.

If this cube were inside a sphere, such that every corner of the cube touched the inside of the sphere, then the length of segment CD would also be the diameter of the sphere. How's that for multitasking?

Example Problem

To show you how you could put this theory into practice, let's look at an example SAT problem. In the cube shown, point B is at the center of the bottom face of the cube. What is the length of line segment AB (not shown)? It's a tough nut to crack, but we can make it work with triangles. Here's how.

First, think of the line segment AB as the longest side of a right triangle, like below. We already have one side of the triangle, which is 6. But we need the other side, the distance from the corner of the square to point B.

To find that, we'll use another triangle. Since all the sides of a cube are the same, we can find the legs of this triangle and then solve for the hypotenuse using the Pythagorean theorem.

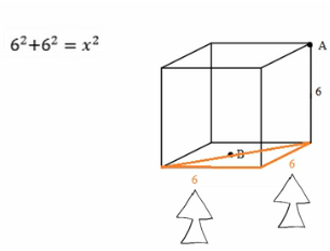
6^2 + 6^2 = x^2, so x^2 = 72. That makes x equal to 6(sqrt2). B is right in the middle of the bottom face, so we'll cut this in half to find the distance just from the corner to B: it's 3(sqrt2). Now see what we have? A right triangle with two known sides.

We can solve for the third to get the distance from A to B: (3*sqrt2)^2 + 6^2 = x^2. So we know that x^2 = 54. We can simplify the square root of 54 to 3(sqrt6). And now we have our answer. Perfectly possible. It just takes some clever use of triangles to make it happen.

Cylinders

As well as hiding triangles in cubes and spheres, the SAT will also ask you questions about cylinders, but here, again, you can crack the problem by breaking the cylinder down into 2-D shapes. If you think about a cylinder, it's really a rectangle rolled into a circle with caps at both ends. If this doesn't make any sense, think about an ordinary tin can. The top and bottom are circles, and if you peel away the label carefully, you'll end up with a rectangular piece of paper. So a cylinder is really just two circles plus a rectangle. Not so scary after all.

To illustrate this, let's look at an example problem. A pencil is to be fit inside a tin can 12 inches tall with a volume of 300 pi inches cubed. What is the length of the longest pencil that will fit completely within the can?

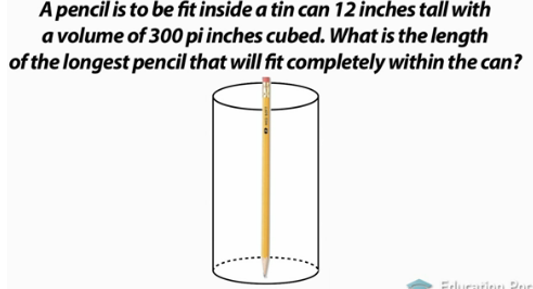
We'll start by drawing a picture. Here's what we're talking about. You can see the cylinder made of two circles and a rectangle and how the pencil fits into the can to maximize the possible length of the pencil. You can fit a lot more pencil into this can by tilting it sideways than by angling it straight up and down.

Now we'll fill in the dimensions we have. The height is 12 inches, and the volume is 300 pi inches cubed. Just like a cube or a rectangular prism, the volume of a cylinder is equal to the area of the base times the height. The only difference is that here, the area of the base is a circle and not a square. Otherwise the formula is the same.

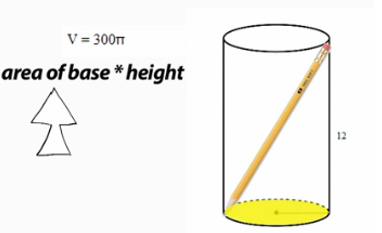
So we'll plug this in: 300 pi = (area of the base)(12). Divide both sides, and we get 25 pi = area of the base. We know that the area of a circle equals pi times the radius squared, so we can solve to get a radius of 5. Can you guess what happens next?

That's right: it's hidden triangles again! There's a nice, friendly right triangle hiding in this cylinder once we figure out the diameter of the base. Just remember to use the diameter instead of the radius since the bottom side of our triangle stretches all the way across the base.

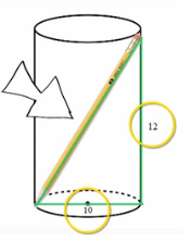
We know that one side of this triangle equals 10, one side is 12, and the third side is the length of the pencil, so we'll just use the Pythagorean theorem to figure it out: 10^2 + 12^2 must equal x^2, so x is the square root of 244, which we can simplify as 2(sqrt61). Triangles to the rescue once again!

Lesson Summary

3-D geometry doesn't have to be painful or impossible. In fact, it doesn't even have to be 3-D! You can do a lot with 3-D shapes by breaking them down. Cubes become collections of squares, cylinders become circles plus rectangles, and pretty much everything has a hidden triangle (or two) that you can use to help you figure out the missing measurements.

All of this might seem like you'll never get a handle on it for yourself, but just think of it as a learned skill. You won't be great at it the first few times, but just keep looking at 3-D shapes this way, and eventually you won't be able to look at them without mentally breaking them down into digestible, 2-D pieces.