Measurements of Lengths Involving Tangents, Chords and Secants

Measurements of Lengths Involving Tangents, Chords and Secants

The lengths of chords, tangents and secants take on unique relationships when they're drawn on circles. In this lesson, we'll define those relationships and see them in action.

Circles are Magic

David Copperfield, Harry Houdini, Penn and Teller, Gob Bluth... the list of famous magicians (or should I say illusionists) goes on and on. Let's add circles to that list.

Wait, circles? How are circles magic? Circles are magic because of their amazing properties. In this lesson, we're going to look at some lines. Without circles, they'd be boring lines, nothing more. You know how things like rabbits, handkerchiefs and boxes with people in them become way more interesting when a magician is around? That's like lines and circles. Let's find out how.

Intersecting Chords

Here are two intersecting lines. Meh. I know. But what if we add a circle like this? Now they're not just lines, they're chords. A chord is a line segment with endpoints on a circle. That's just a warm-up trick, turning lines into chords.

When chords intersect on a circle, they take on a special relationship involving their lengths. Please see that there's nothing up my sleeves. Ok, in our example here, we can prove that AE * EB = CE * ED. So if AE is 6, EB is 3 and CE is 8, we can call ED x and say 6 * 3 = 8x. 6 * 3 is 18, so x equals 18 divided by 8, which is 2.25. Voila!

What can you do with this magic? You can always find the length of a missing chord segment if you know the other three. Ok, it's not getting out of a straightjacket while submerged in a tank of water, but it's still pretty cool.

Let's break the magician's code and understand how this trick works. First, draw lines AC and DB. Now we have two triangles. Now we know that angles CAE and EDB are congruent, as are angles ACE and EBD. Why? Because they're inscribed angles intercepting the same arc, and those are always congruent.

Since we have two pairs of congruent angles, then the triangles are similar. And in similar triangles, the sides are in proportion. So AE/ED = CE/EB. Cross multiply, and you get AE * EB = CE * ED. Whoa

Two Secants

Let's try a similar trick. This time we're looking at secants. A secant is a line that intersects two or more points on a curve. Wait, without a curve, they aren't secants; they're just lines. And lines aren't magic. Let's add a circle.

Secants within a circle

Ok, now these lines take on a special relationship since they're officially secants on a circle and they share an external endpoint. Note that I've never met these secants before tonight. We're going to take a whole secant, AC, and multiply it by its external segment, AB. Is everybody with me? Good. Now we're going to do the same with the other secant: AE * AD.

And guess what? AC * AB = AE * AD. So if AB is 6 and AC is 10, and we also know that AD is 5, what is AE? Let's call AE x. So our equation is 6 * 10 = 5x. That's 60 = 5x. 60 divided by 5 is 12. So AE is, wait for it, 12!

Secants and Tangents

Can you handle one more? Ok, first, I'll make one secant disappear. In its place, we have a tangent line. A tangent is a line that intersects a curve at only one point.

For my final trick, I'm going to multiply the whole secant, AD, by the external segment, AC. Then, I'm going to square the tangent line, AB. So we have AD * AC and we have AB^2. Keep your eyes on the two expressions. Pay no attention to the smoke and mirrors.

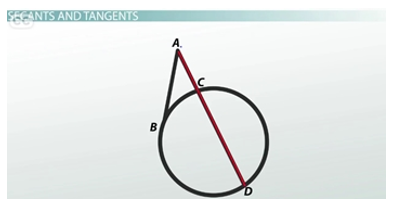
Secant and a Tangent

And now we have this: AD * AC = AB^2

Wait, you might be asking, can we see this in action? Of course! Let's say AB is 6 and AC is 3. What is AD?

So 6^2 = 3x, where x is AD. 6^2 is 36. 36/3 is 12. So AD is 12. Yep, that happened.

Lesson Summary

In summary, circles are magic. More importantly, the lengths of lines on circles have unique relationships.

With intersecting chords, the product of the chord segments equal each other. So in this example, AE * EB = CE * ED.

With two secants that share an endpoint, the product of an external segment and the entire secant equals the product of the other external segment and its entire secant. So in this example, AC * AB = AE * AD

Finally, with a tangent and a secant that share an endpoint, the product of the secant and its external segment equals the tangent squared. So in this example, AD * AC = AB^2.

Thanks for coming. Enjoy the buffet! I'll be here all week.