Congruency of Right Triangles: Definition of LA and LL Theorems

Congruency of Right Triangles: Definition of LA and LL Theorems

In this lesson, we'll learn two theorems that help us prove when two right triangles are congruent to one another. The LA theorem, or leg-acute, and LL theorem, or leg-leg, are useful shortcuts for proving congruence.

Right Triangles

Right triangles aren't like other, ordinary triangles. Ordinary triangles just have three sides and three angles. They're like the random people you might see on a street. They can be tall and skinny or short and wide. There's no order or consistency.

Right triangles are consistent. They always have that clean and neat right angle. They're like a marching band. Sure, there are drummers, trumpet players and tuba players. But they all have those same uniforms, and they march in organized patterns.

And think about the uniform of a right triangle. There's the hypotenuse. It's always the longest side, and it's always in the same place, opposite the 90 degree angle. Then there are the legs. These are the other two sides. They meet to form the 90-degree angle.

When we're trying to prove congruency with triangles, right triangles like to save us a step, so to speak. Other triangles require three matches. There's the side-angle-side postulate, the angle-side-angle postulate and others. Right triangles say, 'Hey, we're already in uniform and in a line. We'll help you out.'

The LA Theorem

Let's start with the LA theorem. The LA Theorem is my theory about how Los Angeles traffic is, wait, hang on...this LA has nothing to do with Los Angeles. The LA in LA theorem refers to leg-acute. It states that if the leg and an acute angle of one right triangle are congruent to the corresponding leg and acute angle of another right triangle, then the triangles are congruent.

Whew. That theorem takes about as long to explain as it takes to get anywhere in LA traffic. I'm pretty sure marching bands would move more quickly on the 405. As for the LA theorem, when you think about it, it's very logical.

Let's look at two triangles, ABC and DEF.

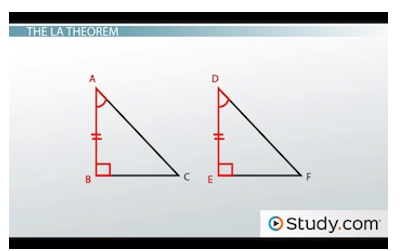
Example triangles

They definitely look like they belong in a marching band together, don't they? We know that they're both right triangles. Angles B and E are each 90 degrees. And we know AB is congruent to DE and angle A is congruent to angle D.

Using the LA theorem, we could say, 'Ok, two right triangles. And we've got a leg and an acute angle that match, so they're congruent.' But why is this true?

Notice that since B and E are congruent, too, that this is really just the angle-side-angle postulate. The fact that they're right triangles just gives us a shortcut. It's like being born with a trumpet already in your hands. Hmm, maybe that's not a good idea.

But even if we didn't have included sides, like AB and DE here, it would still be just like ASA. What if we know A and D are congruent, but then BC and EF? Well, since the sum of the interior angles of a triangle is 180, we know that C and F must also be congruent to each other. So we still get our angle-side-angle.

The LL Theorem

Next, let's talk about the LL theorem. The LL Theorem is about a Maine-based sporting goods retailer...wait, no. That's LL Bean. Different thing. The LL theorem is the leg-leg theorem. LA theorem is leg-acute, so it makes sense that LL is leg-leg. It states that if the legs of one right triangle are congruent to the legs of another right triangle, then the triangles are congruent.

This is like marching bands with their matching pants. Their legs look alike, right?

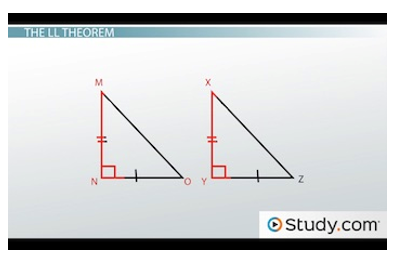
Example triangles

Maybe MNO plays the trombone and XYZ plays the xylophone. We know they're right triangles. Angles N and Y are each 90 degrees. If we know that MN is congruent to XY and NO is congruent to YZ, then we have two legs. This enables us to say they're congruent based on the LL theorem.

The LL theorem is really just the SAS postulate, or side-angle-side. Remember that the legs of a right triangle always meet at a right angle, so we always know the included angle between them.

Using the Theorems

So we've learned about the LA, or leg-acute, theorem and the LL, or leg-leg, theorem. These are complemented by the HA and HL theorems. The HA theorem is the hypotenuse-angle theorem, and the HL theorem is the hypotenuse-leg theorem. (Check out the lessons on these other two theorems for more on each.) Let's look at a few triangles and see how we can determine congruency.

Two triangles formed from a rectangle

This is what happens when two band members march into each other. Be careful not to get hit with a French horn. Are they congruent? Well, we say that angles OLN and MNL are congruent. And they share a hypotenuse. Therefore, we can say that they are congruent based on the HA, or hypotenuse-angle theorem.

They don't immediately look congruent. They look like marchers marching in different directions. But note that BC is congruent to ST, and angles A and R are congruent. Therefore, we can use the LA theorem to determine that they are congruent. This is that example where we aren't exactly given the angle-side-angle, but we know that angles B and S must also be congruent.

Here are another two that go their own way:

Maybe the woodwinds finally got sick of the brass. Anyway, AB and YZ are congruent. So are BC and XZ. Are those two pairs of legs? No, AB and YZ are each across from the right angle. What's across from a right angle? The hypotenuse. So we have a hypotenuse and a leg. Guess what? That's the HL, or hypotenuse-leg, theorem.

Ok, time for one more. Here are two triangles that look like they're in some kind of formation:

Maybe this is one of those bands that is choreographed to make cool shapes. Ok, what do we know? FH is congruent to LK. And HG is congruent to JK. Those are all legs. Matching pants are abounding here. Legs and legs? That's the leg-leg, or LL, theorem.

Lesson Summary

In summary, we learned about two useful right triangle congruency theorems.

First, there's the LA theorem. This is the leg-acute theorem. It states that if the leg and an acute angle of one right triangle are congruent to the corresponding leg and acute angle of another right triangle, then the triangles are congruent.

Next, we learned about the LL theorem. This is the leg-leg theorem. This one states that if the legs of one right triangle are congruent to the legs of another right triangle, then the triangles are congruent.

We also learned to apply these theorems in establishing congruency with right triangles. They complement two other right triangle theorems, the hypotenuse-angle, or HA, theorem and the hypotenuse-leg, or HL, theorem.