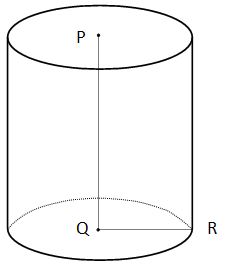
Right Cylinders
A right circular cylinder has two circular bases of equal size whose centers are both perpendicularly intersected by the same line. In the diagram below, the surface with point P and the surface with point Q are both the same size. Surface P and surface Q are both perpendicularly intersected by line PQ, making these surfaces parallel.
Volume = (area of base) × (height)
V = pr2h where r is the radius, which is QR in the above diagram
In other words, the volume is equal to the area of the base multiplied by the height.
Consider the following example:
What is the area of the figure above if PQ = 5 and QR = 3?
V = (p32)(5) = 9p(5) = 45p
Surface Area
Surface Area = 2(pi)(radius)2 + 2(pi)(radius)(height)
SA = 2(pr2) + 2prh
In other words, the surface area is equal to the summation of the area of each of the faces. For example, if a right circular cylinder had a radius of 3 and height of 5, then SA = 2(p × 9) + 2p × 3 × 5 = 18p + 30p = 48p