Geometry Circles

A circle is all points in the same plane those lie at an equal distance from a center point. The circle is only composed of the points on the border.

The distance between the midpoint and the circle border is called the radius. A line segment that has the endpoints on the circle and passes through the midpoint is called the diameter. The diameter is twice the size of the radius. A line segment that has its endpoints on the circular border but does not pass through the midpoint is called a chord.

The distance around the circle is called the circumference, C, and could be determined either by using the radius, r, or the diameter, d:

C = 2pr

C = pd

A circle is the same as 360°. You can divide a circle into smaller portions. A part of a circle is called an arc and an arc is named according to its angle. Arcs are divided into minor arcs (0° < v < 180°), major arcs (180° < v < 360°) and semicircles (v = 180°).

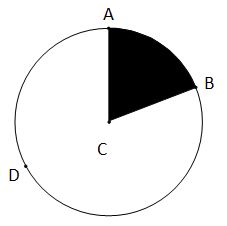
Arcs

An arc is a portion of the edge of a circle. For example, the portion of the circle between A and B is called arc AB. The length of the arc is proportional to the central angle that forms the arc (i.e., angle ACB in this example).

In the above diagram, if radius CB is 9cm and angle ACB is 60°, what is the length of arc AB? Find the circumference

C = 2p(9) = 18p

Plug into the length of an arc formula

(60/360)(18p)

(1/6)(18p)

3p

Sectors

A sector is a portion of the area of a circle. For example, the portion of the circle between center C and arc AB forms a sector (this sector is shaded in black below). The area of the sector is proportional to the central angle that forms it.

In the figure above, if radius CA is 9cm and angle ACB is 60°, what is the area of the region shaded in black?

Find the area

A = p(9)2 = 81p

Plug into the area of a sector formula

(60/360)81p

(1/6)(81p)

(81/6)p

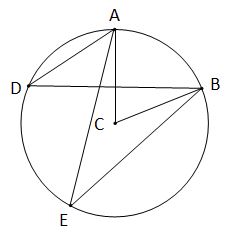
Inscribed Angle and Central Angle

A central angle is an angle whose vertex is the center of the circle and whose endpoints are the edge of the circle. Angle ACB is a central angle. An inscribed angle is an angle whose vertex lies on the edge of the circle and whose endpoints lie on another part of the edge of the circle. Angle ADB and angle AEB are both examples of inscribed angles.

For a central angle and an inscribed angle with the same endpoints:

All inscribed angles with the same endpoints are equal

ADB = AEB

Inscribed Angle = (1/2)(Central Angle)

ADB = (1/2)ACB

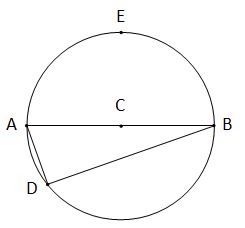
Inscribed Triangle

As a result of the equality mentioned above between an inscribed angle and half of the measurement of a central angle, the following property holds true: if a triangle is inscribed in a circle such that one side of that triangle is a diameter of the circle, then the angle of the triangle that is opposite the diameter is a right angle.

The reason that angle ADB is a right angle is because central angle ACB is 180° and ADB is an inscribed angle whose endpoints are the same as ACB.

Consequently:

ADB = 1/2(ACB)

ADB = 1/2(180) = 90

For the above to hold true: (1) C must be the center of the circle (2) AB must be a diameter of the center

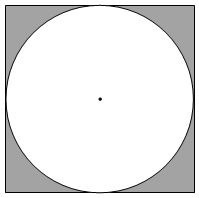
Inscribed Circle

An inscribed circle is a circle that lies inside a figure such that points on the edge of the circle are tangent to the sides of the figure. For example, the following is a circle inscribed in a square.

Circumscribed Circles

A circumscribed circle is a circle that encompasses a polygon such that the circle touches all the vertices of the polygon. The following is a circle circumscribed around a rectangle.