Properties of All Triangles

A triangle is a three-sided shape whose three inner angles must sum to 180°. The largest angle will be across from the longest side while the smallest angle will be across from the shortest side of the triangle. If and only if two sides of a triangle are equal, the angles opposite them will be equal as well.

Sum of Angles is 180

The sum of the interior angles in any triangle is 180°

Triangle Inequality Theorem

The sum of any two sides of a triangle must be greater than the third side of a triangle.

For example, the figure below is not physically possible since the sum of two sides is smaller than the third side.

Longest Side Opposite Largest Angle

The longest side of a triangle is opposite the largest angle of a triangle. Conversely, the smallest side of a triangle is opposite the smallest angle of a triangle. Consider the following example:

Rank the size of the angles of triangle ABC from largest to smallest.

• Since side AC is the longest side, angle B is the largest angle.
• Since side AB is the next longest side, angle C is the next largest angle.
• Since side BC is the shortest side, angle A is the smallest angle.

Exterior Angle Theorem

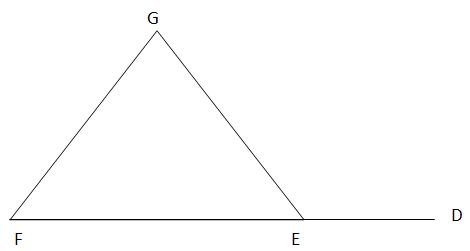
The exterior angle theorem states:

Angle EFG + Angle EGF = Angle DEG

Consider the following example:

In the figure above, if angle EFG is 60° and angle DEG is 120°, what is the measure of angle FGE?

Angle EFG + Angle EGF = Angle DEG

60 + Angle EGF = 120

Angle EGF = 60

Types Triangles

• Right Triangle One angle is 90°
• Scalene Each side has a different length
  Each angle has a different measurement
• Obtuse One angle of the triangle is greater than 90°
• Acute Every angle of the triangle is less than 90°
• Equilateral Every angle of the triangle is equal (i.e., 60°)
  Every side of the triangle is equal in length
• Isosceles Two angles of the triangle are equal
  Two sides of the triangle are equal in length

Similar Triangles

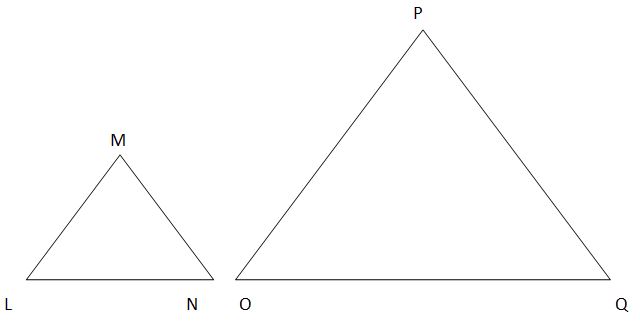
When Are Triangles Similar?

Two triangles are similar if any one of the following three possible scenarios is met:

1. AAA [Angle Angle Angle] - The corresponding angles of each triangle have the same measurement. In other words, the above triangles are similar if:
   Angle L = Angle O; Angle N = Angle Q; Angle M = Angle P
2. SAS [Side Angle Side] - An angle in one triangle is the same measurement as an angle in the other triangle and the two sides containing these angles have the same ratio. In other words, the above triangles are similar if:
   Angle L = Angle O; Side LM/Side OP = Side LN/Side OQ
   Note: Any other combination of side, angle, side also proves similarity.
3. SSS [Side Side Side] - Each pair of corresponding sides have the same ratio. In other words, the above triangles are similar if:
   Side LM/Side OP = Side LN/Side OQ = Side MN/Side PQ

Properties of Similar Triangles

1. Corresponding angles are the same measurement.
2. The perimeter of each triangle is in the same ratio as the sides.
3. Corresponding sides are all in the same proportion.

Congruent Triangles

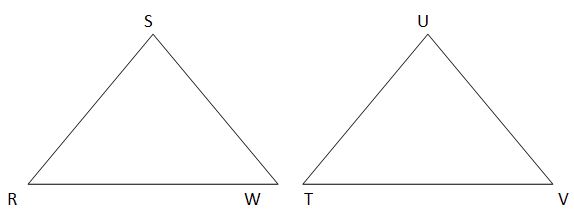
When Are Triangles Congruent?

Two triangles are congruent if any one of the following three possible scenarios is met:

1. SAS [Side Angle Side] - Two pairs of corresponding sides are equal and the corresponding angle between the sides is equal. In other words, the above triangles are congruent if:
   Side SW = Side UV; Angle W = Angle V; Side WR = Side VT
   Note: Any other combination of side, angle, side also proves congruence.
2. ASA [Angle Side Angle] - Two pairs of corresponding angles are equal and the corresponding side between them is equal. In other words, the above triangles are congruent if:
   Angle R = Angle T; Side RW = Side TV; Angle W = Angle V Note: Any other combination of angle, side, angle also proves congruence.
3. SSS [Side Side Side] - All three pairs of corresponding sides are equal. In other words, the above triangles are congruent if:
   Side RS = Side TU; = Side RW = Side TV; Side SW = Side UV

Properties of Congruent Triangles

Corresponding angles have the same measurement.

Corresponding sides have the same measurement.

Area of a Triangle

The area of a triangle is given by the following formula:

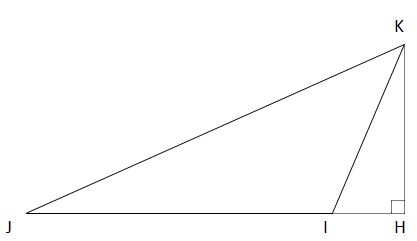
Area = 1/2(base)(height)

The height of the triangle is the length of the line which is perpendicular to the base and goes through the opposite vertex (i.e., line KH in the triangle below).

To reiterate, the area of a triangle can be found using the equation: A = 1/2bh. In this case, b stands for the base of the triangle and h stands for the height. Any side can be chosen to be the base, but the height is the line that is perpendicular to the base and goes through the opposing vertex. The perimeter of a triangle is the sum of the three sides.

Consider the following example:

Referring to the triangle immediately above, what is the area of triangle KIJ if KJ = 13, KH = 5, IH = 3, and JI = 9?

Area = 1/2(JI)(HK)

Area = 1/2(9)(5) = 22.5