Lesson: Data Sufficiency Basic - 17t01

Data Sufficiency : Practice A Yes/No Question

Now let’s try a yes/no question. Use the CAT Method to select your answer, then click Continue.

Is x > 1?

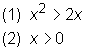
	Statement (1) BY ITSELF is sufficient, but statement (2) by itself is not sufficient.
	Statement (2) BY ITSELF is sufficient, but statement (1) by itself is not sufficient.
	Both statements TAKEN TOGETHER are sufficient, but NEITHER statement BY ITSELF is sufficient.
	EACH statement BY ITSELF is sufficient.
	The two statements TAKEN TOGETHER are NOT sufficient.

Countinue

Focus on the question stem.

• A statement has to show that x is definitely, or definitely not, greater than 1 to be sufficient.
• Note that we may not need the exact value of x, we just need to know whether x is greater than 1.
• Pay attention to what the stem does not say. The stem does not state that x is an integer so don’t forget fractions as you consider each statement.

Statement (2) is shorter, so begin there. The statement declares that x > 0 but that does not guarantee that x is greater than 1. Don’t forget fractions; x could be . Is x > 1? Maybe. Thus, Statement (2) is insufficient so we can eliminate Choices (B) and (D).

Now consider Statement (1): Don’t fall into the trap of dividing each side of the inequality by x! (Remember, you must know whether a quantity is positive or negative before you multiply or divide each side of an inequality. Multiplying or dividing by a negative number will change the direction of the inequality.) Pick numbers instead.

Remember that the statements are always facts. So you must pick numbers that conform to the conditions in Statement (1). For example, 0, 1, and 2 would not be permissible numbers to pick because they would make the statement false. Use 3 and –3 (Negative 3 is permissible — don’t add information from Statement 2 to your evaluation of Statement (1)).

When x = 3 the answer to the question is "Yes." However, when x = –3 the answer to the question is "No." So, Statement (1) is insufficient and we can eliminate Choice (A).

Since each statement is insufficient separately, go to Step 3 of the CAT Method, and combine the statements.

In combination the two statements read:

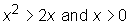
Since you know that x is positive, divide each side of the inequality in Statement (1) by x. That leaves x > 2. If x > 2, then x must also be greater than 1. So, the answer to the question is "Yes" and the answer is Choice (C).

Next to display next topic in the chapter.