What is Slope Intercept Form? - Definition,

What is Slope Intercept Form? - Definition, Equation & Examples

The slope-intercept form is one of several ways you can write the equation of a line. In this lesson, you will learn about the definition and equation of the slope-intercept form and work through some real-world examples.

Introduction: Developing the Cost Equation for a Cupcake Store

A friend of mine opened a cupcake store called Wild About Cupcakes. She has a storefront where she bakes all the cupcakes and sells them. She hired two employees to help her bake and sell. She asked me to help her determine the daily cost for her business. After some analysis, I figured out that whether she bakes a single cupcake or not, there is a fixed daily cost of $550. This amount includes employee salaries, rent, etc. There is also a variable cost that changes with the number of cupcakes baked. The variable cost is $1.25 per cupcake. This amount includes the cost of ingredients, liners, etc. If x is the number of cupcakes baked and y is the total daily cost then:

y = 1.25x + 550

The table below shows sample values for x and y.

The graph for y = 1.25x + 550 is shown below.

Observations:

1. Each additional cupcake produced incurs an incremental cost of $1.25.
2. With no cupcakes produced (x = 0), there is still a cost of $550 (y = 550).
3. The graph of y = 1.25x + 550 crosses the y-axis at the point (0, 550).

Definition and Equation

The equation of the total daily cost function for Wild About Cupcakes is in the form:

y = mx + b

where m = 1.25 and b = 550. The graph of the equation y = mx + b (where m and b are real numbers) is a line with slope, m, and y-intercept, b. This form of the equation of a line is called slope-intercept form.

The slope of a line, m, is a measure of its steepness. As we have seen in the Wild About Cupcakes example, it is also a measure of how much y changes for every unit increase in x.

Given any two points on a line, (x1, y1) and (x2, y2), the formula to calculate the slope is shown below.

The y-intercept of a line, b, is the y-coordinate of the point where the graph of the line crosses the y-axis. As we have seen in the Wild About Cupcakes example, it is the value of y when x = 0.

Examples: Finding the Slope-Intercept Form of the Equation of a Line

1. Two points on line L are (0, -1) and (3, -3). What is the slope-intercept form of the equation of L?

Answer:

The slope-intercept form of the equation of a line is y = mx + b, where m is the slope of the line, and b is the y-intercept. Since we are given two points, we can calculate the slope m as follows:




Note that the slope is the same if we interchange the order of the points.




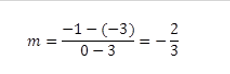
We know that the y-intercept, b = -1 since the line crosses the y-axis at the point (0, -1). Also, remember that the y-intercept, b, is the value of ywhen x = 0.

Therefore, the equation of the line with m = -2/3 and b = -1 is given by:

y = (-2/3)x – 1

2. A line has equation:

iy - 2 = (-1/2)(x + 3)

What is the equation of this line in slope-intercept form?

Answer:

The given equation is in slope-point form, that is:

y - y1 = m(x - x1)

where m is the slope of the line and (x1, y1) is a point on the line. We can use algebraic operations to convert it to slope-intercept form.




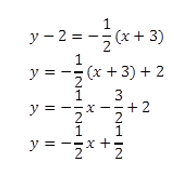
The last equation above is in slope-intercept form. The slope is m = -1/2, and the y-intercept is b = 1/2.

Examples: Real-World Applications of Slope-Intercept Form

3. In physics, an object moving in a straight line with constant acceleration will have a final velocity, v, given by the equation:

v = at + u

where a is the constant acceleration, u is the initial velocity and t is the elapsed time. This equation is known as a kinematic equation. Notice that this equation is in slope-intercept form, y = mx + b. In the comparison of the two equations below, corresponding variables and constants are shown with the same color.

In the kinematic equation, t is your x variable, v is your y variable, a is the slope and u is the y-intercept.

Suppose an object has an initial velocity of 18 m/s (meters per second) and is accelerating at -3 m/s^2 (meters per second squared). The negative acceleration value simply means that the object is slowing down or decelerating. What is the velocity of the object after 4 s (seconds)?

Answer:

Here we can use the kinematic equation, v = at + u with a = -3 and u = 18. At elapsed time t = 4 s:

v = (-3)(4) + 18 = 6 m/s

Note that the object has slowed down from 18 m/s to 6 m/s in 4 seconds.

4. With $10 in my pocket, I decided to take a taxi from the Chicago Union Train Station to my workplace, a total distance of 3.75 miles. The taxi charges a flat amount of $2.25 plus $0.45 per quarter mile traveled. What is the equation (in slope-intercept form) that relates the number of quarter miles traveled and total cost of the taxi ride? Did I have enough money for the ride?

Answer:

We need an equation that relates the number of quarter miles traveled and the total cost of the taxi ride. Let x = number of quarter miles traveled, and y = total cost of taxi ride. We can write our equation in slope-intercept form as:

y = 0.45x + 2.25

where the slope, m = 0.45, and the y-intercept, b = 2.25. The total distance between the train station and my workplace is 3.75 miles or 15 quarter miles (Note: there are fifteen ¼ miles in 3.75 miles). Therefore, the total cost for the taxi ride is:

y = 0.45(15) + 2.25 = $9.

Yes, I had enough money for the ride.

Below is the graph for the equation y = 0.45x + 2.25. The point (15, 9) is plotted on the graph, which shows that I could have gone a little over 17 quarter miles with my $10!