Let's look at the following vertical line and try and find m.
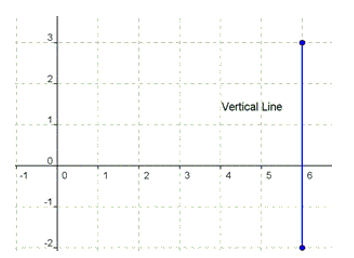
According to the slope equation we need to have two points. Luckily, we can choose any points on the line shown above. Let's use the points (6,0) and (6,2). Now, plug those into your slope equation and see what you get!
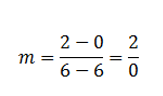
Once we do the calculations, we get the slope to be 2/0. But there is a problem here. Do you see it?
The slope in this case violates a huge rule in mathematics. We cannot divide by zero! Try any two points on any vertical line and you would run into the same problem. So you see, a vertical line does not have a slope!
If our line doesn't have a slope, then how do we write an equation? Take a look at the points from our example above. What two values are the same?
The answer, of course, is the sixes! In fact, pick any point on that line and I bet you are going to have a six in the x position. This is because the x-value determines where the line is located.
For our example, x = 6 describes the entirety of the line. As you can see by looking at it, no matter what the y-value is, x will always be six.
Every vertical line works exactly the same way. They have no slope and their function is in the form x = #, where # is whatever x-value the line goes through.
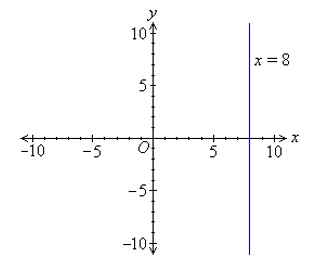
In this example the x-values are all eight, so the equation of the line is x = 8.
Summary
Vertical lines are different than any other line. They have no slope. This can be seen by trying to calculate the slope of any vertical line. Vertical lines are also represented by x = instead of y =. To write the equation of a vertical line, find the x value in which the line passes through and then set x = to that value. If the line passes through the x values of three, then the equation is x = 3.