Roots and Powers of Algebraic Expressions

Simplify Square Roots of Quotients

The quotient rule can be used to simplify square roots of quotients. This lesson will define the quotient rule and show you how it is used to simplify square roots.

The Quotient Rule

The quotient rule for radicals says that the radical of a quotient is the quotient of the radicals, which means:

Solve Square Roots with the Quotient Rule

You can use the quotient rule to solve radical expressions, like this. Simplify:

We can't take the square root of either of these numbers, but we can use the quotient rule to simplify the expression.

75 divided by 3 is 25, which we can take the square root of. .

Let's try another one.

We can use the quotient rule to simply this expression. .

x^3 divided by x is x^2. .

We can take the square root of x^2. .

And x is the answer. .

Rationalize the Denominator

There are occasions when you will simplify a fraction with a radical and still end up with a square root in the denominator. When this happens, there is one more step you will have to do to complete the problem, and that is rationalize the denominator. .

The first step is to use the quotient rule to make one fraction under the square root symbol. .

We can simplify this fraction because both numbers are divisible by 3. This reduces the fraction to 5/2. Since there is still a fraction under the radical symbol, we must rationalize the denominator to fully simplify the expression. To do this, first return the expression to a division problem containing two square roots using the quotient rule. .

Now you need to multiply the numerator and denominator of the fraction by a number that will eliminate the radical in the denominator of the fraction. Remember, multiplying both the numerator and denominator of a fraction by the .

same number is like multiplying by 1, so you're not really changing the fraction. For this example, the number to multiply by is the square root of 2.

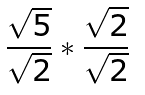
When you do this, you get: .

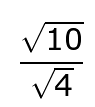
Since the square root of 4 is 2, we can simplify one more step, leaving the answer without a radical in the denominator. .

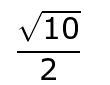
Let's try one more example. Simplify: .

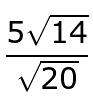
First, we use the quotient rule to simplify the fraction. .

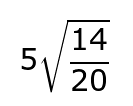
Then simplify, if possible. .

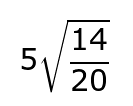
Return the fraction to one containing a square root in the numerator and one in the denominator in order to rationalize the denominator. .

Multiply the numerator and denominator by the square root of 10. .

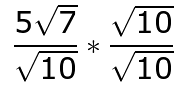
The square root of 100 can be simplified to 10. .

Since there is a 5 and a 10 outside the radical symbols, they can be reduced to give the final answer of: .

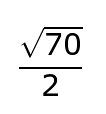
Lesson Summary

In order to simplify square roots of quotients, we use the quotient rule, which says that if you have a fraction with a radical in both the numerator and denominator, they can be simplified by placing them both under the same radical .

symbol. If the fraction itself cannot be simplified, the problem is still not completed unless there is no square root in the denominator of the fraction. To remove a radical from the denominator, you must use a process called 'rationalizing the denominator.' This process will not change the value of your expression but will help to rewrite it without using a square root in the denominator of the fraction. .