Roots and Powers of Algebraic Expressions

Signed Number in Math: Definition & Examples

In this lesson, we will find out about signed numbers. The use of signed numbers could be thought of as where arithmetic ends and algebra begins. We will also discuss situations encountered every day that can be described by using signed numbers.

What Are Signed Numbers?

We will begin an introduction to signed numbers with what is known as the number line. A number line is a horizontal line with incremental marks indicating the position of numbers. The conventional layout for all number lines will have the positive numbers are on the right, the negative numbers are on the left and zero between the negative numbers and the positive numbers. The signed numbers consist of the negative numbers and the positive numbers. We are not used to seeing the (+) sign on positive numbers and most of the time it is not necessary to show it. However, it is always necessary to show the sign on a negative number.

Notice that for every positive number, there is a negative counterpart. This is true no matter how small or how large the number is. These counterparts are the same distance from zero. For example, the number 5 and -5 are the same distance from zero. The number 0.0001 and -0.0001 are both the same distance from zero. The number 100,000 and -100,000 are the same distance from zero.

A more precise description for these counterparts is to say that they are opposites or additive inverses. Every number on the number line except zero has an opposite or additive inverse, and it is found by simply changing the sign of the number. The numbers 5 and -5 are opposites or additive inverses. Zero is not considered either negative or positive.

Comparing Values of Signed Numbers

In arithmetic, we learned how to compare positive numbers. We know, for example, that 2 is less than 5. Looking at these values on the number line, we see that 2 is to the left of 5. In fact, notice that the numbers become less in value as you move to the left on the number line and the numbers become greater in value as you move to the right on the number line.

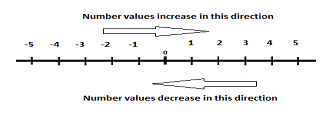
This relationship remains true for numbers on the negative side of the number line as well. For example, -2 is greater in value than -5 because it is farther to the right on the number line.

You have to be especially careful comparing negative fractions and decimals but the same principle applies: numbers farther to the left are less in value and numbers farther to the right are greater in value. For example, -2/3 is less than -1/3 while on the positive side of zero 2/3 is greater than 1/3.

How Are Signed Numbers Used in Mathematics?

It may be difficult at first to understand how anything can be less than zero or nothing. The following examples may illustrate that this concept is useful when considering numbers below zero in a relative or comparative sense rather than absolute.

Consider the following scenario: You borrow $50 from a friend and agree to pay the friend back $10 each month. Since debt is money you owe and will be paid out, it can't really be considered +$50, since this would indicate money you have received. A more accurate value for the money you owe would be -$50. Each time you pay $10, this would take away from the debt and bring you closer to owing $0. Thus, you start your debt on the left side of zero at -$50, and as you pay your friend, the value of the debt would move right by $10 dollars until you owed $0.

As a second example, consider a temperature of 5 degrees on a winter day. Suppose the weather man says that the temperature will drop 10 degrees overnight. Looking at the number line, we can see that a drop of 5 degrees will take the temperature to zero. To indicate a drop of more than 5 degrees, you need numbers below zero.

As a third example, the level of land on the surface of the earth may be described as being at sea level, or some point either above sea level or below sea level. Sea level is generally considered a position of 0 miles elevation from the surface of the earth. Death Valley in California is said to have an elevation of 282 feet below sea level. Instead of using the phrase 'below sea level,' this could also be described as -282 relative to sea level. Likewise, the highest

point of elevation in the United States is reportedly 14,505 feet, meaning 14,505 feet above sea level. Like most positive numbers, the (+) sign is usually not shown but rather is understood to represent a number above 0.

Lesson Summary

The signed numbers consist of the positive numbers and their opposites or additive inverses, which are the negative numbers. Negative numbers are less than zero. Every number on the number line except zero has an opposite or additive inverse. On the number line, any number to the right of another is greater in value and any number to the left of another is less in value. The concept of less than zero may be difficult to understand at first. It may be easier to understand when this concept is used in a comparative or relative sense rather than absolute.