The Photoelectric Effect
Electromagnetic radiation transmits energy, so when visible light, ultraviolet
light, X rays, or any other form of electromagnetic radiation shines on a piece
of metal, the surface of that metal absorbs some of the radiated energy. Some of
the electrons in the atoms at the surface of the metal may absorb enough energy
to liberate them from their orbits, and they will fly off. These electrons are
called photoelectrons, and this phenomenon, first noticed in 1887, is
called the photoelectric effect.
The Wave Theory of Electromagnetic Radiation
Young’s double-slit experiment, which we looked at in the previous chapter,
would seem to prove conclusively that electromagnetic radiation travels in
waves. However, the wave theory of electromagnetic radiation makes a number of
predictions about the photoelectric effect that prove to be false:
|
Predictions of the wave theory |
Observed result |
|
Time lapse |
Electrons need to absorb a certain amount of wave energy before they can be
liberated, so there should be some lapse of time between the light hitting the
surface of the metal and the first electrons flying off.
Electrons begin flying off the surface of the metal almost instantly after light
shines on it.
Intensity
The intensity of the beam of light should determine the kinetic energy of the
electrons that fly off the surface of the metal. The greater the intensity of
light, the greater the energy of the electrons.
The intensity of the beam of light has no effect on the kinetic energy of the
electrons. The greater the intensity, the greater the number of electrons that
fly off, but even a very intense low-frequency beam liberates no electrons.
Frequency
The frequency of the beam of light should have no effect on the number or energy
of the electrons that are liberated.
Frequency is key: the kinetic energy of the liberated electrons is directly
proportional to the frequency of the light beam, and no electrons are liberated
if the frequency is below a certain threshold.
Material
The material the light shines upon should not release more or fewer electrons
depending on the frequency of the light.
Each material has a certain
threshold frequency: light with a lower
frequency will release no electrons.
Einstein Saves the Day
The young Albert Einstein accounted for these discrepancies between the wave
theory and observed results by suggesting that electromagnetic radiation
exhibits a number of particle properties. It was his work with the photoelectric
effect, and not his work on relativity, that won him his Nobel Prize in 1921.
Rather than assuming that light travels as a continuous wave, Einstein drew on
Planck’s work, suggesting that light travels in small bundles, called photons,
and that each photon has a certain amount of energy associated with it, called a
quantum. Planck’s formula determines the amount of energy in a given
quantum:
E = hƒ
where h is a very small number,6.63 × 10-34
J · s to be precise, called Planck’s constant, and
f is the frequency of the beam of
light.
Work Function and Threshold Frequency
As the wave theory correctly assumes, an electron needs to absorb a certain
amount of energy before it can fly off the sheet of metal. That this energy
arrives all at once, as a photon, rather than gradually, as a wave, explains why
there is no time lapse between the shining of the light and the liberation of
electrons.
We say that every material has a given work function,
F,
which tells us how much energy an electron must absorb to be liberated. For a
beam of light to liberate electrons, the photons in the beam of light must have
a higher energy than the work function of the material. Because the energy of a
photon depends on its frequency, low-frequency light will not be able to
liberate electrons. A liberated photoelectron flies off the surface of the metal
with a kinetic energy of:
KE = hƒ - F
Example
Two beams of light, one blue and one red, shine upon a metal with a work
function of 5.0 eV. The frequency of the blue light is
6.5 × 1014
Hz, and the frequency of the red light is
4.0 × 1014
Hz. What is the energy of the electrons liberated by the two beams of light?
In order to solve this problem, we should translate h from units of J · s
into units of eV · s:
h = (6.63 × 10-34J.s)(1eV/1.6 × 10-19J) = 4.14 × 10-15eV.s
We know the frequencies of the beams of light, the work function of the metal,
and the value of Planck’s constant, h.
Let’s see how much energy the electrons liberated by the blue light have:
KE = hƒ - F = (4.14 × 10-5 eV.s)(6.5 × 1014Hz) - 5.0 eV = 2.7 eV
For the electrons struck by the red light:
KE = hƒ - F = (4.14 × 10-5 eV.s)(4.0 × 1014Hz) - 5.0 eV =
3.3 eV
The negative value in the sum means that
F > hƒ,
so the frequency of the red light is too low to liberate electrons. Only
electrons struck by the blue light are liberated.
The Bohr Model of the Atom
Let’s now return to our discussion of the atom. In 1913, the Danish physicist
Niels Bohr proposed a model of the atom that married Planck’s and Einstein’s
development of quantum theory with Rutherford’s discovery of the atomic nucleus,
thereby bringing quantum physics permanently into the mainstream of the physical
sciences.
The Problem with Rutherford’s Model
Light and other electromagnetic waves are emitted by accelerating charged
particles. In particular, the electrons being accelerated in orbit about the
nucleus of an atom release a certain amount of energy in the form of
electromagnetic radiation. If we recall the chapter on gravity, the radius of an
object in orbit is a function of its potential energy. If an electron gives off
energy, then its potential energy, and hence the radius of its orbit about the
nucleus, should decrease. But according to Rutherford’s model, any radiating
electron would give off all its potential energy in a fraction of a second, and
the electron would collide with the nucleus. The fact that most of the atoms in
the universe have not yet collapsed suggests a fundamental flaw in Rutherford’s
model of electrons orbiting nuclei.
The Mystery of Atomic Spectra
Another puzzling phenomenon unexplained by Rutherford’s model, or anything else
before 1913, is the spectral lines we see when looking through a spectroscope.
A spectroscope breaks up the visible light emitted from a light source into a
spectrum, so that we can see exactly which frequencies of light are being
emitted.
The puzzling thing about atomic spectra is that light seems to travel only in
certain distinct frequencies. For instance, we might expect the white light of
the sun to transmit light in an even range of all different frequencies. In
fact, however, most sunlight travels in a handful of particular frequencies,
while very little or no light at all travels at many other frequencies.
Bohr’s Hydrogen Atom
Niels Bohr drew on Rutherford’s discovery of the nucleus and Einstein’s
suggestion that energy travels only in distinct quanta to develop an atomic
theory that accounts for why electrons do not collapse into nuclei and why there
are only particular frequencies for visible light.
Bohr’s model was based on the hydrogen atom, since, with just one proton and one
electron, it makes for the simplest model. As it turns out, Bohr’s model is
still mostly accurate for the hydrogen atom, but it doesn’t account for some of
the complexities of more massive atoms.
According to Bohr, the electron of a hydrogen atom can only orbit the proton at
certain distinct radii. The closest orbital radius is called the electron’s
ground state. When an electron absorbs a certain amount of energy, it will
jump to a greater orbital radius. After a while, it will drop spontaneously back
down to its ground state, or some other lesser radius, giving off a photon as it
does so.

Because the electron can only make certain jumps in its energy level, it can
only emit photons of certain frequencies. Because it makes these jumps, and does
not emit a steady flow of energy, the electron will never spiral into the
proton, as Rutherford’s model suggests.
Also, because an atom can only emit photons of certain frequencies, a
spectroscopic image of the light emanating from a particular element will only
carry the frequencies of photon that element can emit. For instance, the sun is
mostly made of hydrogen, so most of the light we see coming from the sun is in
one of the allowed frequencies for energy jumps in hydrogen atoms.
Analogies with the Planetary Model
Because the electron of a hydrogen atom orbits the proton, there are some
analogies between the nature of this orbit and the nature of planetary orbits.
The first is that the centripetal force in both cases is
F = mv2/r
.
That means that the centripetal force on the electron is directly proportional
to its mass and to the square of its orbital velocity and is inversely
proportional to the radius of its orbit.
The second is that this centripetal force is related to the electric force in
the same way that the centripetal force on planets is related to the
gravitational force:
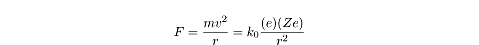
where e is the electric charge of
the electron, and Ze is the electric
charge of the nucleus. Z is a
variable for the number of protons in the nucleus, so in the hydrogen atom,
Z = 1.
The third analogy is that of potential energy. If we recall, the gravitational
potential energy of a body in orbit is
U = Gm1m2/r.
Analogously, the potential energy of an electron in orbit is:
.gif)
Differences from the Planetary Model
However, the planetary model places no restriction on the radius at which
planets may orbit the sun. One of Bohr’s fundamental insights was that the
angular momentum of the electron, L,
must be an integer multiple of
h/2p.
The constant
h/2p
is so common in quantum physics that it has its own symbol,
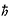 .
If we take n to be an integer, we
get:L = mvr = nh
.
If we take n to be an integer, we
get:L = mvr = nh
Consequently,
v = n /mr .
By equating the formula for centripetal force and the formula for electric
force, we can now solve for r:
/mr .
By equating the formula for centripetal force and the formula for electric
force, we can now solve for r:
.gif)
Don’t worry: you don’t need to memorize this equation. What’s worth noting for
the purposes of
Physics is that there are certain constant values for
r, for different integer values of
n. Note also that
r is proportional to
n2,
so that each successive radius is farther from the nucleus than the one before.
Electron Potential Energy
The importance of the complicated equation above for the radius of an orbiting
electron is that, when we know the radius of an electron, we can calculate its
potential energy. Remember that the potential energy of an electron is
U = -k0(e)(Ze)/r.
If you plug in the above values for r,
you’ll find that the energy of an electron in a hydrogen atom at its ground
state (where n =
1 and Z
= 1) is –13.6
eV. This is a negative number because we’re dealing with potential
energy: this is the amount of energy it would take to free the electron from its
orbit.
When the electron jumps from its ground state to a higher energy level, it jumps
by multiples of n. The potential
energy of an electron in a hydrogen atom for any value of
n is:

Frequency and Wavelength of Emitted Photons
As we said earlier, an excited hydrogen atom emits photons when the electron
jumps to a lower energy state. For instance, a photon at
n = 2 returning to the ground state
of n = 1 will emit a photon with
energy
E = (-3.4eV) - (13.6eV) = 10.2eV .
Using Planck’s formula, which relates energy and frequency, we can determine the
frequency of the emitted photon:
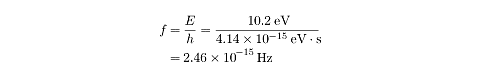
Knowing the frequency means we can also determine the wavelength:
? = c/ƒ = 1.22 × 10-7
As it turns out, this photon is of slightly higher frequency than the spectrum
of visible light: we won’t see it, but it will come across to us as ultraviolet
radiation. Whenever an electron in a hydrogen atom returns from an excited
energy state to its ground state it lets off an ultraviolet photon.
Example
A hydrogen atom is energized so that its electron is excited to the n = 3
energy state. How many different frequencies of electromagnetic radiation could
it emit in returning to its ground state?
Electromagnetic radiation is emitted whenever an electron drops to a lower
energy state, and the frequency of that radiation depends on the amount of
energy the electron emits while dropping to this lower energy state. An electron
in the n =
3 energy state can either drop to
n = 2
or drop immediately to n =
1. If it drops to
n = 2,
it can then drop once more to n =
1. There is a different amount of energy
associated with the drop from n =
3 to n
= 2, the drop from
n = 3
to n =
1, and the drop from n =
2 to n
= 1, so there is a different frequency of
radiation emitted with each drop. Therefore, there are three different possible
frequencies at which this hydrogen atom can emit electromagnetic radiation.
Wave-Particle Duality
The photoelectric effect shows that electromagnetic waves exhibit particle
properties when they are absorbed or emitted as photons. In 1923, a French
graduate student named Louis de Broglie (pronounced “duh BRO-lee”) suggested
that the converse is also true: particles can exhibit wave properties. The
formula for the so-called de Broglie wavelength applies to all matter,
whether an electron or a planet:
? = h/mv
De Broglie’s hypothesis is an odd one, to say the least. What on earth is a
wavelength when associated with matter? How can we possibly talk about planets
or humans having a wavelength? The second question, at least, can be easily
answered. Imagine a person of mass 60 kg,
running at a speed of 5 m/s. That person’s
de Broglie wavelength would be:

We cannot detect any “wavelength” associated with human beings because this
wavelength has such an infinitesimally small value. Because
h is so small, only objects with a
very small mass will have a de Broglie wavelength that is at all noticeable.
De Broglie Wavelength and Electrons
The de Broglie wavelength is more evident on the atomic level. If we recall, the
angular momentum of an electron is
 .
According to de Broglie’s formula, mv = h/?.Therefore,
hr/? = nh/2p n?= 2pr
.
According to de Broglie’s formula, mv = h/?.Therefore,
hr/? = nh/2p n?= 2pr
The de Broglie wavelength of an electron is an integer multiple of
2pr,
which is the length of a single orbit. In other words, an electron can only
orbit the nucleus at a radius where it will complete a whole number of
wavelengths. The electron in the figure below completes four cycles in its orbit
around the nucleus, and so represents an electron in the
n = 4
energy state.
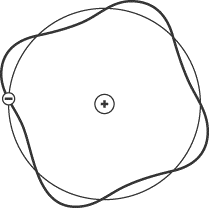
The de Broglie wavelength, then, serves to explain why electrons can orbit the
nucleus only at certain radii.
Example
|
|
|
Which of the following explains why no one has ever managed to observe and
measure a de Broglie wavelength of the Earth? |
|
(A) |
The Earth is traveling too slowly. It would only have an observable de Broglie
wavelength if it were moving at near light speed. |
|
(B) |
The Earth is too massive. Only objects of very small mass have noticeable
wavelengths. |
|
(C) |
The Earth has no de Broglie wavelength. Only objects on the atomic level have
wavelengths associated with them. |
|
(D) |
“Wavelength” is only a theoretical term in reference to matter. There is no
observable effect associated with wavelength. |
|
(E) |
The individual atoms that constitute the Earth all have different wavelengths
that destructively interfere and cancel each other out. As a result, the net
wavelength of the Earth is zero. |
This is the sort of question you’re most likely to find regarding quantum
physics on
Physics: the test writers want to make sure you understand the
theoretical principles that underlie the difficult concepts in this area. The
answer to this question is B. As we discussed above, the wavelength of an
object is given by the formula
?
= h/mv. Since
h is such a small number,
mv must also be very small if an
object is going to have a noticeable wavelength. Contrary to A, the
object must be moving relatively slowly, and must have a very small mass. The
Earth weighs
5.96 × 1024
kg, which is anything but a small mass. In fact, the de Broglie wavelength for
the Earth is
3.71 × 10-64
m, which is about as small a value as you will find in this book.
Heisenberg’s Uncertainty Principle
In 1927, a young physicist named Werner Heisenberg proposed a counterintuitive
and startling theory: the more precisely we measure the position of a particle,
the less precisely we can measure the momentum of that particle. This principle
can be expressed mathematically as:
?x?p = h/4p
where
?x
is the uncertainty in a particle’s position and
?p
is the uncertainty in its momentum.
According to the uncertainty principle, if you know exactly where a
particle is, you have no idea how fast it is moving, and if you know exactly how
fast it is moving, you have no idea where it is. This principle has profound
effects on the way we can think about the world. It casts a shadow of doubt on
many long-held assumptions: that every cause has a clearly defined effect, that
observation has no influence upon experimental results, and so on. For
Physics, however, you needn’t be aware of the philosophical conundrum Heisenberg
posed—you just need to know the name of the principle, its meaning, and the
formula associated with it.
Back
Next
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.