What is a System of Equations

What is a System of Equations

So what happens if we want to compare more than one equation? Welcome to a 'system' of equations! Learn what one is, how to solve them and when they come up in real life.

Comparing and Contrasting

Comparing and contrasting is something that comes up in all school subjects and also in real live too. Maybe you're taking an English class that asks you to write an essay that compares and contrasts 'The Wizard of Oz' and 'Huckleberry Finn.' Or maybe you're taking a world history class that asks you to talk about the similarities and differences between World War I and World War II. Math is the same way; sometimes one equation can be good enough for all the information we're trying to find, but it's often true that we want to compare multiple equations at the same time. Any time we do have more than one equation in a single problem, it's called a system of equations, and that's what this lesson is all about.

Comparing the Speed of Two Runners

So I'd like to give you an example of a system of equations, but I'm going to start with a little background information first.

I like to run. I go out every once in a while and I've even been in a few races. I actually did a triathlon a few years ago too. But my girlfriend is actually a huge runner and she runs almost every day. We decided it would be fun to do a race together so we started running with each other to get ready for it, but we quickly realized that she was way faster than I was. So to keep it interesting for both of us, we decided to give me a little bit of a head start and see if she could catch me.

This represents a system of equations because we have two equations - one that represents me and one that represents her. When we solve it, we're trying to figure out when these equations are the same.

Now we can do this two ways, either with a graph or with algebra. Just like always, the graph is going to provide us with a good visual estimate, but the algebra is going to do a much better job of telling us an exact answer.

Graphing a System of Equations

So let's go ahead and start with the graph first so we can get an idea of what's going on and maybe make a guess about what we think, and then we'll use the algebra later to check our guess.

If we start by graphing me first, I'm going to start already 2 miles ahead even after zero minutes have gone by, so my first point is up here at 2 miles. Then every 1 mile I go up, I have to go 9 minutes over, so my next point would be right here. Then I would go up another mile over 9 minutes and my next point would be right here. We can keep going up 1 mile over 9 minutes and we get a bunch of points in a row.

But I'm not just magically teleporting between points; I'm kind of slowly making it there. So between these points there are a bunch of little dots. I'm kind of slowly making it to that point and if you put enough little dots in a row, they end up turning into a solid line. What we end up with is a straight line that says exactly where I am after a certain number of minutes.

The reason it's a straight line is because we're assuming that I can go the same speed the whole time. I never slow down and I never speed up. It's a linear equation. I'm always increasing by the same amount every time.

Graph of a system of equations

Her equation begins down at zero because she doesn't get a head start. She starts down here at zero, but then every 1 mile she goes up, she only has to go over 7 minutes. So if we continue that pattern, we get a bunch of little points in a row; we connect all the points and we get a line for her as well.

And what we're looking for is where she catches me, which is where the lines intersect; the spot where they're in the same place. It appears to be right here. So it looks like she's going to beat me, but let's go ahead and check back with the algebra.

Setting Up a System of Equations

So because both of these equations are lines, that means they're linear equations, which means I can write them in slope-intercept form (mx+b). So the only two things I need for find for each equation is the slope (how much we're moving by) and the y-intercept (where we begin).

If we do my equation first, my beginning point is at 2 miles because I get a 2-mile head start. So my b value is 2. The slope, which is the rise over the run, is up 1 mile and over 9 minutes.

So my slope is 1/9, which means my equation is y = (1/9)x+2.

She, on the other hand, doesn't get a head start, so her y-intercept is zero. We could put a 'plus zero' on the end or we could just not write it at all. Her slope, how much she's moving by (the rise over the run), is she's going up 1 mile and over 7 minutes each time. Her slope is 1/7. Her equation is y = (1/7)x.

Solving for x in the system of equations

Solving a System of Equations

Since we're trying to find where these two equations are the same, we just want to know at what point are the ys and the xs the same. So if I want the ys to be the same - if I want my y to be the same as her y - what I can do is simply substitute what I know my yis in for her y. So where I see her y, I put what my yis. This means I take the expression (1/9)x+2 and put it where her y was. I get a new equation, which is (1/9)x+2 = (1/7)x. Now I have a linear equation with one variable that I can solve using inverse operations.

I can undo the (1/9)x with subtraction over to the other side. I have to do some fraction subtraction, so I have to do (1/7)x minus (1/9)x, which means getting a common denominator. (9/63)x minus (7/63)x gives me (2/63)x.

On the other side of the equation, we still have our 2. We now need to undo a fraction. I can undo a fraction by multiplying by its reciprocal. So I multiply both sides by 63/2. The x is now by itself and 2*63/2, using some fraction multiplication, tells us that x is equal to 63.

If we refer back to our graph, we see that the x-axis is minutes, and so we have just found that she is going to catch me in 63 minutes. But we're not exactly sure if that's before or after we've finished the 13 miles, so to find out where on the track that was, we have to substitute 63 back in to either equation. It actually doesn't matter which one because we're in the same spot, so we'll get the same answer either way.

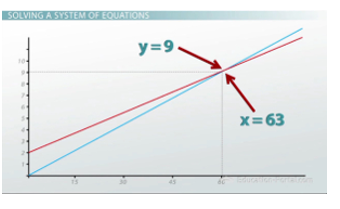
Solving the system reveals the exact point where the runners meet up

I'll choose to plug it into hers because it's a little bit easier (we don't have to add the 2 on the end). And I get y = (1/7)*63. Doing another quick fraction multiplication problem, we end up with y = 9 miles. This means it took her 63 minutes to catch me and we were 9 miles into the race, so she totally beat me.

Lesson Summary

To review, a system of equations is any problem that has more than one equation in it. When we solve a system of equations, we're finding the point where those equations are the same. That means that if we graph the system, and we try to solve it using the graph, we find where the two lines intersect. The intersection point is our solution.

Whereas if we want to try solving it with algebra, we can use what's called the substitution method. If we know what one variable is, we can substitute the expression for one variable in for that same variable in the other equation and then solve the resulting equation.