Solving Linear Inequalities: Practice Problems

Solving Linear Inequalities: Practice Problems

Linear inequalities may look intimidating, but they're really not much different than linear equations. In this lesson, we'll practice solving a variety of linear inequalities.

Greater or Lesser

Greater than and less than. These two symbols can be quite controversial. It all depends on what you put on either side. What if I said hot sauce is greater than ketchup? Or, cats are less than dogs? Or, the Denver Broncos are greater than the New England Patriots? These are debatable points. I mean, I think they're all true, and I'd argue them passionately, but they're really just opinions.

But, what if I said 6 > 7? Well, that's just wrong. 6 < 7. And, so are other numbers, including 5, 4, 3... well, the list just goes on from there. There's no debate. And, in this lesson, we're going to practice handling these types of situations.

Linear Inequalities

You've already seen linear equations like this: x - 2 = 0. You solve for x, and get x = 2. Our variable, x, has a single value that we can determine. That's straightforward but also a little dry. It's like finding out that hot sauce is hot sauce and not comparing it to any potentially inferior condiments.

But, then there are linear inequalities. A linear inequality is a linear expression that contains relational symbols. That means that instead of =, you'll see >, <, >, or <. So, instead of our variable standing in for a single value, it's standing in for a relational value, as in x > 2, where x is all values greater than 2.

Basic Practice

Let's solve some basic linear inequalities, then try a few more complicated ones. Just as with linear equations, our goal is to isolate the variable on one side of the inequality sign.

First, what about this: x + 5 > 9. We treat this just like we would if we had x + 5 = 9. We subtract 5 from both sides. Now we have x > 4. On a number line, that would look like the image below, where x is all numbers larger than, but not equal to, 4.

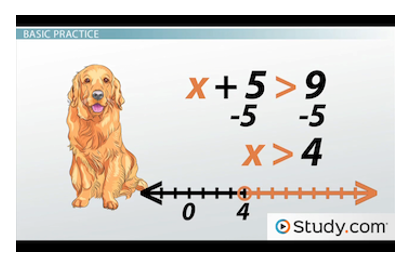
In this problem, x is all numbers greater than 4.

Note what x + 5 > 9 looks like. Here, the phrase 'x + 5' can be shown as all numbers greater than 9. So, all we did was take that 5 away, which shifted our line so it looks like the image above.

Here's another: 18 < 12 + x. Okay, again, get the variable alone. Subtract 12 from both sides, and we have 6 < x. We could flip that around to say x > 6. Just remember that if you do that, don't forget to flip the inequality sign! That one looks like this:

In this problem, 6 is less than x.

Here's one: x - 7 < 1. Let's add 7 to both sides to get x < 8. This graph looks like this:

Fill in the circle around 8 because the sign means less than or equal to 8.

Note that we fill in the circle around the 8 because xisn't just less than 8, it's less than or equal to 8. Xcould be all these values as well as 8 - no sense making 8 feel left out.

Let's do one more basic one: x + 11 > 14. This time, we subtract 11 from both sides, which gives us x > 3. If we graph that, we get this line:

In this problem, x is greater than or equal to 3.

Again, we have a solid circle because x is greater than or equal to 3.

Advanced Practice

That's enough of the basic ones. Those are all like saying chocolate ice cream is greater than vanilla. Pretty straightforward, right? Okay, maybe in some circles.

Here's a trickier one: 3x - 6 < 9. Let's start by adding 6 to both sides. Now we have 3x < 15. What do we do? Remember, it's just like a linear equation. If we had 3x = 15, we'd divide both sides by 3. We do the same thing here. That gives us x < 5. That's it!

Here's another kind we haven't seen before: 7x + 2 < 8 + 5x. It looks more complicated, but the principle of getting that variable all alone hasn't changed. First, let's subtract 2 from both sides. Now, let's move the 5x over by subtracting 5x from both sides. Now we have 2x < 6. Just like the last one, we divide. So, we have x < 3. And, we did it.

There is one key rule that makes solving linear inequalities different than solving linear equations: if you multiply or divide by a negative number, you must reverse the inequality.

Let's see this in action: -2x < 8. This time, we divide by negative 2. So, we flip the sign. Now we have x > -4.

Does this make any sense? Well, if x > -4, what could x be? How about 1? If x = 1, is -2x < 8? Let's see. It'd be -2(1), which is -2. Is -2 < 8? Yes. We could keep trying this with all of the infinite numbers greater than -4, or you could trust me that it will always work. I say trust me. Otherwise, this lesson will be really long.

Let's solve one more: -12x - 3 < 19 - x. Let's start by adding 3 to both sides. 19 becomes 22. Now let's add the x to both sides. -12x becomes -11x. Finally, we'll divide by -11. That means flipping the sign. And, 22 becomes -2. It's important to not forget that negative sign. We're flipping the sign, but otherwise the normal rules of solving equations still apply. So, we have x > -2.

Lesson Summary

In summary, solving a linear inequality is just like solving a linear equation. The big difference is that instead of your variable being equal to a single number, like x = 10, it's defined in relation to a number. We use four symbols: >, <, > and <. When solving, we treat it as though the inequality sign were an equal sign. There's just one exception: If you're multiplying or dividing by a negative number, the sign gets flipped.