Linear Inequality: Solving,

Linear Inequality: Solving, Graphing & Problems

If you can solve linear equations, you can solve linear inequalities. In this lesson, you will learn how similar the solving processes are. You will also learn the notations you need to use when graphing linear inequalities.

What Is a Linear Inequality?

A linear inequality is very similar to a linear equation. Recall that a linear equation has variables to the first degree only, and the variables are never squared, cubed, or taken to any other power. Your linear equations might have looked something like these:

Linear inequalities look very similar. Instead of equal signs, though, linear inequalities have inequality symbols much like these:

So, linear inequalities only have variables to the first power and have inequality symbols. Now let's learn how to solve linear inequalities.

How to Solve

Think back to when you last solved a linear equation. Do you remember the steps you took? If you were given a problem such as x + 2 = 6, you most likely looked at it and realized that you need to move the number 2 to the other side of the equation so that your variable is alone. So, you proceeded to subtract 2 from both sides of the equation remembering that to keep an equation equal, whatever you do to one side you also must do to the other. After subtracting 2 from both sides, your variable is alone and you have solved the linear equation. Your answer is x = 4.

Now, let's say you are given a problem like x + 2 < 6. You first notice that, instead of an equal sign, you have an inequality sign. This tells you that it is a linear inequality problem. To solve, you use very similar steps to those of solving linear equations. You notice that the 2 is on the same side as your variable. So to move the 2, you subtract it from both sides. The inequality sign remains the same. Your answer is x < 4. To tell someone the answer, you would say: The solutions are all numbers less than 4.

The inequality sign gives you a range of numbers that are all your solutions. To test a solution, plug it into the inequality and, if the statement remains true, the solution is valid. For example, if you plug in a 1 into the statement x < 4, it becomes 1 < 4. You know that 1 is definitely less than 4, so the statement remains true and 1 is a valid solution.

Practice

Let's try a practice linear inequality:

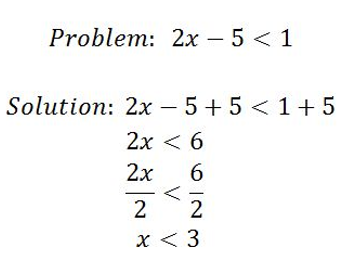
To solve, we must isolate the variable by adding 5 to both sides. Then we divide both sides by 2 so that the variable is by itself. The resulting solution is x < 3, or all numbers less than 3.

Dividing by Negatives

There is one tricky aspect to solving linear inequalities, and that is when you are dividing or multiplying by a negative number. Whenever this is the case, the inequality symbol flips sides.

Remember this - it's an easily forgotten rule.

For example:

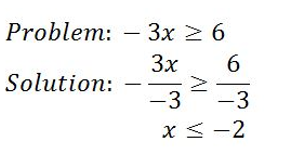
You first solve the inequality by dividing each side of the inequality by -3. This gives you x greater than or equal to -2. Now, flip the symbol to get your solution: x less than or equal to -2. Remember, flip the inequality symbol whenever you divide or multiply by a negative number.

How to Graph

Graphing linear inequalities requires a few more steps than graphing linear equations. For example, to graph the linear equation x = 4, you would put a solid circle on the number 4 on the number line. For the linear inequality x < 4, you also have a circle on the number 4, but it will be an open circle. In other words, you draw a circle around the number 4. If the inequality was less than or equal to, you would draw a solid circle. To show the inequality part, you then draw a line from the circle to the left showing that all the numbers less than 4 are included.

Graphing a linear inequality such as y > x + 1 is similar to graphing the linear equation form y = x + 1. This is an equation of a line in slope-intercept form, and you graph it similarly. With inequalities, though, if the symbol is either < or >, then you would draw a dashed line instead of a solid line. If the symbol has an equal part in it, then you would draw a solid line.

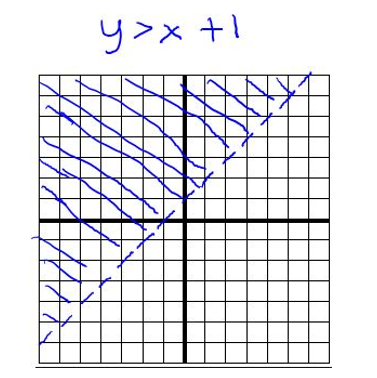
The shaded region accounts for the inequality part. Think about the linear inequality and what it says. It says that y is greater than x + 1. The region above the line gives you y values that are larger, and so that is what gets shaded.

Lesson Summary

Solving linear inequalities is very similar to solving linear equations. The main difference is you flip the inequality sign when dividing or multiplying by a negative number. Graphing linear inequalities has a few more differences. When graphing on the number line, an open circle is for the symbols < and >. A solid circle is for the other two symbols. On the Cartesian graph, a dashed line is for the symbols < and >. To represent the other two symbols, a solid line is used. The part that is shaded includes the values where the linear inequality is true.