How to Add, Subtract and Multiply Polynomials

How to Add, Subtract and Multiply Polynomials

Adding, subtracting and multiplying polynomials are, basically, the same as adding, subtracting and multiplying numbers. They only difference is that we have a pesky variable to worry about, but this video will show you that's no problem, so no worries! This method has worked for many of my students, and I think it will work for you, too!

Adding Polynomials

Use shapes to organize like terms in the polynomials.

Adding polynomials is very easy! There are many ways to add polynomials that have been taught, but here's my favorite. I look at the problem and put a circle, square or triangle around the like terms so I don't get them confused.

Let's look at this example.

(2x^2 + 3x + 4) + (x^2 - 5x + 7)

I like to start from the left. I circle 2x^2. Now, I look for another like term to 2x^2. Of course, that's x^2, so I circle it.

Then I add them: 2x^2 + x^2 is 3x^2, and then I write that down as part of my answer.

The next term is 3x. I put a square around that one. Then look for another one. Of course, we have -5x, so I put a square around that one too.

Then add them: 3x + -5x is -2x, and I write that down as the next part of my answer.

You always want to double check that there aren't any more.

Finally, we have 4. I continue the same idea, but I put a triangle around it. Now I look for another like term to 4. Of course, that's 7, so I put a triangle around that one.

Then I add them: 4 + 7 is 11, and I write that down as the last part of my answer.

It's always good to double check that you have everything in a circle, square or triangle. When you get longer polynomials, it's easy to miss terms!

So here's my final answer: 3x^2 - 2x + 11.

'Okay, Kathryn, do I have to use circles, squares and triangles?' No! If you're good at adding polynomials, you can cross off as you go, but for those that haven't had enough practice, this is definitely my suggestion.

'Kathryn, what about problems that have more terms? What other shapes or ideas do you have?' Great question! You can use different colors to circle like terms. I don't use it here for the benefit of students who are color blind, but you could have used red to circle the x^2s, blue to circle the xs and green for the numbers. I've also used the method of underlining like terms too! Whatever you choose is how you will distinguish the different terms!

Distributing -1 into the second expression turns the subtraction problem into an addition one.

Subtracting Polynomials

In subtraction, let me show you the underlining method.

(3x^2 - 2x + 5) - (2x^2 - 6x + 7)

First, I am going to distribute the -1 into the second expression. That will make this an addition problem!

The first expression stays the same: 3x^2 - 2x + 5. We will distribute the negative, like this: -1 * 2x^2, which is -2x^2; -1 * -6x, which is a positive 6x; and -1 * 7, which is -7. This gives us our new subtraction problem: (3x^2 - 2x + 5) + (-2x^2 + 6x - 7).

Remember, I am going to show you the method of underlining instead of circling to add the expressions.

We look at the first term 3x^2 and underline it. Now, I continue to look for a like term. Here it is, -2x^2, and I underline it. Now I add them: 3x^2 + (-2x^2), and we get x^2. That's going to be the first term of our answer.

he second term is -2x, and this time, I put a squiggly line under it. Now I continue to look for a like term. Here it is: 6x, and I put a squiggly line under that one. I add -2x + 6x, and I get 4x. That's the second term in our answer.

The last term is 5, and this time I put a jagged line under it. Now, I continue to look for a like term. Here it is: -7, and I underline it. Now, I add them: 5 + -7, and we get -2. This will be my last term in the answer: x^2 + 4x -2.

Multiply the first term in the product, x, by everything in the second expression.

Multiplying Polynomials

Now, we get to multiplication. This problem won't quite work like addition or subtraction, and we can't use FOIL because these are larger than a binomial times a binomial!

(x+5)( x^2+3x-2)

First, multiply the first term in the product: x times everything in the second expression.

I like to draw arrows to remind me which multiplication I've done; otherwise I tend to get lost.

This is how it will look:

x(x^2) + x(3x) + x(-2)

Let's multiply.

x(x^2) = x^3 + x(3x) = 3x^2 + x(-2)= -2x.

This isn't our final answer; we need to multiply everything in the second expression by 5!

So we'll have 5(x^2) + 5(3x) + 5(-2)

Are you ready for the final answer? We simply add the like terms together!

x^3 + 3x^2 - 2x + 5x^2 + 15x – 10

Start from the left, and circle x^3. It looks like there aren't any like terms for x^3, so we write that down as our final answer.

Put a square around 3x^2. I look and find 5x^2, so I put a square around that term, too. I don't see any more, so 3x^2 + 5x^2 = 8x^2. 8x^2 is written next to x^3 as part of our final answer.

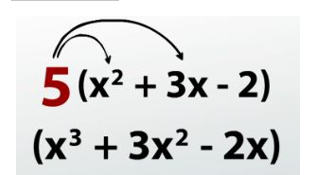
Before getting the final answer, multiply all terms in the second expression by 5.

Put a triangle around -2x. I look and find 15x, so I put a triangle around that term too. Why? Well, they're like terms. I don't see any more like terms for -x, so -2x + 15x = 13x. 13x is part of our final answer, and I'm going to write it next to 8x^2.

Finally, I see -10. I underline this term and look for another one like it. I don't see one, so -10 is written in my final answer.

So, what is the final answer then?

x^3 + 8x^2 + 13x - 10.

Lesson Summary

Adding: No trick here. Just add like terms together. If you get lost at first, use circles, squares, triangles, lines...anything to separate the different terms.

Subtraction: Multiply the second expression by -1, and add the two expressions together.

Multiplication: Multiply each term in the first expression by each term in the second expression. Add like terms together and you're done!