For people who believed that light must travel through an ether, the result of
the Michelson-Morley experiment was like taking a ride in a boat and
discovering that the boat crossed the wave crests at the same rate when it was
driving against the waves as when it was driving in the same direction as the
waves.
No one was sure what to make of the Michelson-Morley experiment until 1905, when
Albert Einstein offered the two basic postulates of special relativity and
changed forever the way we think about space and time. He asked all sorts of
unconventional questions, such as, “What would I see if I were traveling at the
speed of light?” and came up with all sorts of unconventional answers that
experiment has since more or less confirmed.
The Basic Postulates of Special Relativity
Special relativity is founded upon two basic postulates, one a holdover from
Newtonian mechanics and the other a seeming consequence of the Michelson-Morley
experiment. As we shall see, these two postulates combined lead to some pretty
counterintuitive results.
First Postulate
The laws of physics are the same in all inertial reference frames.
An inertial reference frame is one where Newton’s First Law, the law of
inertia, holds. That means that if two reference frames are moving relative to
one another at a constant velocity, the laws of physics in one are the same as
in the other. You may have experienced this at a train station when the train is
moving. Because the train is moving at a slow, steady velocity, it looks from a
passenger’s point of view that the station is moving backward, whereas for
someone standing on the platform, it looks as if the train is moving forward.
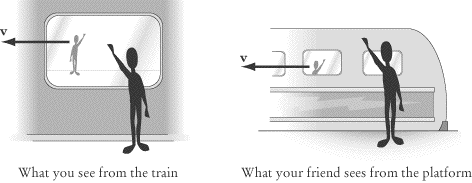
Einstein’s first postulate tells us that neither the passenger on the train nor
the person on the platform is wrong. It’s just as correct to say that the train
is still and the Earth is moving as it is to say that the Earth is still and the
train is moving. Any inertial reference frame is as good as any other.
Second Postulate
The speed of light in a vacuum is a constant—3.0 × 108
m/s—in every reference frame, regardless of the motion of the observer or the
source of the light.
This postulate goes against everything we’ve learned about vector addition.
According to the principles of vector addition, if I am in a car moving at
20 m/s and collide with a wall, the wall
will be moving at 20 m/s relative to me. If
I am in a car moving at 20 m/s and collide
with a car coming at me at 30 m/s, the
other car will be moving at 50 m/s relative
to me.
By contrast, the second postulate says that, if I’m standing still, I will
measure light to be moving at
3.0 × 108
m/s, or hc, relative to me, and if
I’m moving toward the source of light at one half of the speed of light, I will
still observe the light to be moving at c
relative to me.
By following out the consequences of this postulate—a postulate supported by the
Michelson-Morley experiment—we can derive all the peculiar results of special
relativity.
Time Dilation
One of the most famous consequences of relativity is time dilation: time slows
down at high speeds. However, it’s important to understand exactly what this
means. One of the consequences of the first postulate of special relativity is
that there is no such thing as absolute speed: a person on a train is just as
correct in saying that the platform is moving backward as a person on the
platform is in saying that the train is moving forward. Further, both the person
on the train and the person on the platform are in inertial reference frames,
meaning that all the laws of physics are totally normal. Two people on a moving
train can play table tennis without having to account for the motion of the
train.
The point of time dilation is that, if you are moving relative to me in a very
highspeed train at one-half the speed of light, it will appear to me that time
is moving slower on board the train. On board the train, you will feel like time
is moving at its normal speed. Further, because you will observe me moving at
one-half the speed of light relative to you, you will think time is going
more slowly for me.
What does this all mean? Time is relative. There is no absolute clock to
say whether I am right or you are right. All the observations I make in my
reference frame will be totally consistent, and so will yours.
We can express time dilation mathematically. If I were carrying a stopwatch and
measured a time interval,
t0,
you would get a different measure, t,
for the amount of time I had the stopwatch running.
The relation between these measures is:
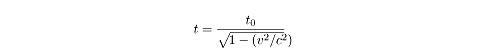
So suppose I am moving at one-half the speed of light relative to you. If I
measure 10 seconds on my stopwatch, you will measure the same time interval to
be:
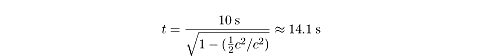
This equation has noticeable effects only at near light speeds. The difference
between t and
t0
is only a factor of
.
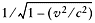This factor—which comes up so frequently in special relativity that it has been
given its own symbol,
?—is
very close to 1 unless
v is a significant fraction of
c. You don’t observe things on a
train moving at a slower rate, since even on the fastest trains in the world,
time slows down by only about 0.00005%.
Time Dilation and Simultaneity
Normally, we would think that if two events occur at the same time, they occur
at the same time for all observers, regardless of where they are. However,
because time can speed up or slow down depending on your reference frame, two
events that may appear simultaneous to one observer may not appear simultaneous
to another. In other words, special relativity challenges the idea of absolute
simultaneity of events.
Example
A spaceship of alien sports enthusiasts passes by the Earth at a speed of 0.8c,
watching the final minute of a basketball game as they zoom by. Though the clock
on Earth measures a minute left of play, how long do the aliens think the game
lasts?
Because the Earth is moving at such a high speed relative to the alien
spaceship, time appears to move slower on Earth from the aliens’ vantage point.
To be precise, a minute of Earth time seems to last:
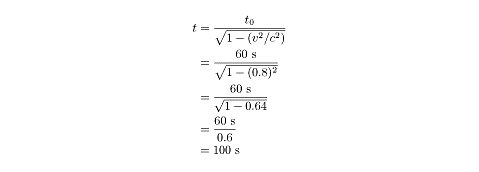
Length Contraction
Not only would you observe time moving more slowly on a train moving relative to
you at half the speed of light, you would also observe the train itself becoming
shorter. The length of an object,
?,
contracts in the direction of motion to a length
?0
when observed from a reference frame moving relative to that object at a speed
v.
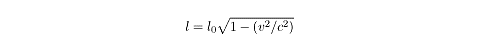
Example
You measure a train at rest to have a length of 100 m and width of 5 m. When you
observe this train traveling at 0.6c
(it’s a very fast train), what is its length? What is its width?
What is its length?
We can determine the length of the train using the equation above:
.gif)
What is its width?
The width of the train remains at 5 m,
since length contraction only works in the direction of motion.
Addition of Velocities
If you observe a person traveling in a car at 20
m/s, and throwing a baseball out the window in the direction of the car’s
motion at a speed of 10 m/s, you will
observe the baseball to be moving at 30
m/s. However, things don’t quite work this way at relativistic speeds. If a
spaceship moving toward you at speed u
ejects something in the direction of its motion at speed
v0
relative to the spaceship, you will observe that object to be moving at a speed
v:
Example
|
|
|
A spaceship flying toward the Earth at a speed of 0.5c fires a rocket at
the Earth that moves at a speed of 0.8c relative to the spaceship. What
is the best approximation for the speed, v, of the rocket relative to the
Earth? |
|
(A) |
v > c |
|
(B) |
v = c |
|
(C) |
0.8c < v < c |
|
(D) |
0.5c < v < 0.8c |
|
(E) |
v < 0.5c |
The most precise way to solve this problem is simply to do the math. If we let
the speed of the spaceship be u =
0.5c and the speed of the rocket
relative to the spaceship be
v0
= 0.8c, then the speed,
v, of the rocket relative to the
Earth is
As we can see, the answer is (C). However, we could also have solved the problem
by reason alone, without the help of equations. Relative to the Earth, the
rocket would be moving faster than 0.8c,
since that is the rocket’s speed relative to a spaceship that is speeding toward
the Earth. The rocket cannot move faster than the speed of light, so we can
safely infer that the speed of the rocket relative to the Earth must be
somewhere between 0.8c and
c.
Mass and Energy
Mass and energy are also affected by relativistic speeds. As things get faster,
they also get heavier. An object with mass
m0
at rest will have a mass m when
observed to be traveling at speed v:
.gif)
Kinetic Energy
Because the mass increases, the kinetic energy of objects at high velocities
also increases. Kinetic energy is given by the equation:
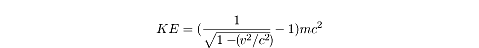
You’ll notice that as v approaches
c, kinetic energy approaches
infinity. That means it would take an infinite amount of energy to accelerate a
massive object to the speed of light. That’s why physicists doubt that anything
will ever be able to travel faster than the speed of light.
Mass-Energy Equivalence
Einstein also derived his most famous equation from the principles of
relativity. Mass and energy can be converted into one another. An object with a
rest mass of
m0
can be converted into an amount of energy, given by:
E = m0c2
We will put this equation to work when we look at nuclear physics.
Relativity and Graphs
One of the most common ways
Physics tests your knowledge of special
relativity is by using graphs. The key to remember is that, if there is a dotted
line representing the speed of light, nothing can cross that line. For instance,
here are two graphs of kinetic energy vs. velocity: the first deals with normal
speeds and the second deals with relativistic speeds:
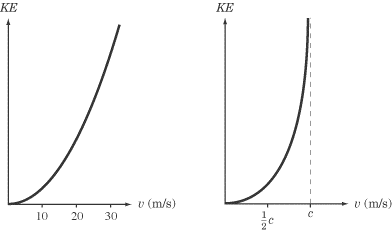
In the first graph, we get a perfect parabola. The second graph begins as a
parabola, but as it approaches the dotted line representing
c, it bends so that it constantly
approaches c but never quite touches
it, much like a y = 1/x graph
will constantly approach the x-axis but never quite touch it.
Back
Next
div>
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.