Properties of Congruent and Similar Shapes

Properties of Congruent and Similar Shapes

In this lesson, we'll look at triangles, rectangles and other shapes that share properties. This includes both congruent and similar shapes. We'll also practice identifying the missing properties of these shapes.

Comparing Shapes

Triangles, rectangles, parallelograms... geometric figures come in all kinds of shapes. This diversity of figures is all around us and is very important. For example, making stop signs octagons and yield signs triangles helps us to differentiate them from a distance.

Figures of the same shape also come in all kinds of sizes. The debit card in your wallet and the billboard on the interstate are both rectangles, but they're definitely not the same size. If they were, you'd either never be able to read that billboard, or your wallet would need to be a really inconvenient size.

When we study figures, comparing their shapes, sizes and angles, we can learn interesting things about them. So, let's get to it!

Congruent Shapes

Sometimes the easiest shapes to compare are those that are identical, or congruent. Congruent shapes are figures with the same size and shape. You could also think of a pair of cars, where each is the same make and model. They're alike in every way. Well, until one gets awesomely tricked out.

For a more geometry-based example of congruency, look at these two rectangles:

These two rectangles are congruent.

We can see that both figures have the same lengths and widths. Next, look at these hexagons:

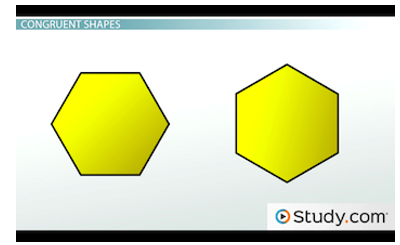
These two hexagons are congruent even though they are not turned the same way.

They aren't turned the same way, but they are congruent. The sides and angles all match. If we took one, turned it and put it on top of the other, you'd see that they match perfectly. That's what being congruent means.

Sometimes, you'll be given special clues to indicate congruency. Let's look at two congruent triangles:

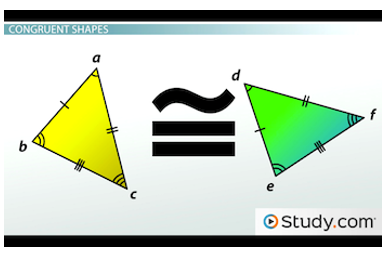
The symbol between the triangles indicates that the triangles are congruent.

When two shapes, sides or angles are congruent, we'll use the symbol above. We know angle A is congruent to angle D because of the symbols on the angles. Likewise, angle B is congruent to angle E, and angle C is congruent to angle F. We also have the hash marks on the triangles to indicate that line AB is congruent to line DE, line BC is congruent to line EF and line AC is congruent to line DF.

Practice with Congruent Shapes

When you have congruent shapes, you can identify missing information about one of them. Consider these two triangles:

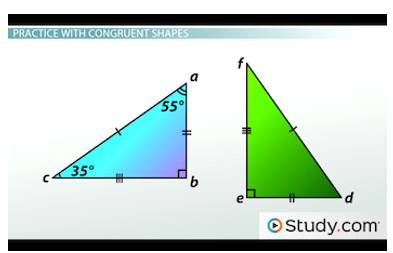
You can use congruency to determine missing information.

We know they're congruent, which enables us to figure out angle F and angle D. We just need to figure out how triangle ABC lines up to triangle DEF. If AB is congruent to DE, and AC is congruent to DF, then angle A is going to be congruent to angle D. So, angle D is 55 degrees. We could use the same logic to determine that angle F is 35 degrees. Or, we could just know that the sum of the interior angles of a triangle is 180, and subtract 55 and 90 from 180 to get 35. Either way, we now know all the angles in triangle DEF.

Sometimes you have even less information to work with. But, you can still figure out quite a bit. Consider these triangles:

There is enough information given by this diagram to determine the remaining angles.

All we're given is the statement that triangle MNO is congruent to triangle PQR. We also know the measures of angles O and Q. This is actually everything we need to know to figure out everything about these two triangles. Use the order of the vertices to guide you. M corresponds to P, N to Q and O to R. So, angle M is congruent to angle P, N to Q and O to R. That means angle R is 50 degrees and angle N is 100 degrees. Since we need the angles to add up to 180, angles M and P must each be 30 degrees.

Similar Shapes

Similar shapes are much like congruent shapes. The key difference is that similar shapes don't need to be the same size. So, similar shapes are figures with the same shape but not always the same size. Remember those two cars we looked at? They're similar. But, so are one car and a Matchbox version. That Matchbox car's the same shape, just much smaller.

Here are two similar rectangles:

Because these rectangles are similar, we can find a missing length.

Notice that the 2/5 is equal to 4/10. If we knew the rectangles were similar, but we didn't know the length of the orange one, we could set up the equation 2/5 = 4/x, and solve for x.

Here are two similar triangles:

Because of the symbol, we know that these two triangles are similar.

Practice with Similar Shapes

Let's try practicing with a few similar shapes. Here are two similar rectangles:

Images for practice example 1

Can you figure out x? You just need to set up a simple equation: 3/6 = 7/x. Cross multiply: 3x = 42. x = 14. We did it!

Here's a pair of triangles:

Images for practice example 2

This time, there are two variables: x and y. Let's start with x. 8/6 = 12/x. 8x = 72. x = 9. Ok, now y. 8/6 = 16/y. 8y = 96. y = 12. That's it!

The properties of similar shapes aren't limited to rectangles and triangles. They work for more complicated shapes, too. Let's say you want to build a scale model replica of the Millennium Falcon from Star Wars in your garage. Why? Why not? The original ship is about 115 feet long and 85 feet wide. Your garage? It's only 24 feet by 20 feet. If you want to make it as big as possible, then you'll make your ship 24 feet long. How wide will it be? 115/24 = 85/x. 115x = 2040. x = 18. So, your ship will be 24 feet by 18 feet. Granted, this leaves you no room to walk around it or fit it through the door, but that's ok. It probably won't fly. Or will it?

Lesson Summary

In summary, congruent shapes are figures with the same size and shape. The lengths of the sides and the measures of the angles are identical. They're exact copies, even if one is oriented differently.

Similar shapes are figures with the same shape but not always the same size. Because the shapes are proportional to each other, the angles will remain congruent. And, you can always find the length of the sides by setting up simple equations.