Perimeter of Triangles and Rectangles

Video Lesson on Perimeter of Triangles and Rectangles

Perimeter of Triangles and Rectangles

Without realizing it, we calculate and use the perimeter of triangles and rectangles in regular everyday situations. Learn more about the perimeter of triangles and rectangles in this lesson, and test your knowledge with a quiz.

The Perimeter

As part of a new fitness program, Melody has to walk around her block three times every day. If each side of her block is 80 ft long, how many feet will she walk every day?

To answer this question, we must find out how many feet are around her entire block, not just one side. This concept is known as the perimeter, which is defined as the distance around an object, shape or figure. To find the perimeter of any polygon, all we have to do is add up the length of all the sides. For this lesson, we will focus on the perimeter of triangles and rectangles, and we'll look at a few examples, beginning with Melody.

Triangle and Rectangle Perimeters

Recall that Melody has to walk around her block three times every day, and each side of her block is 80 ft long. To determine the total length of her walk, we must figure out how many feet are around the entire block. To do so, we'll add 80 + 80 + 80 + 80, since there are four sides to her block. Alternatively, since all of the sides of her block are the same length, we could also multiply 4 * 80. Using either method, we will see that the perimeter of Melody's block is 320. Since she has to circle the block three times, we will add 320 + 320 + 320 to get a total of 960. So, in conclusion, Melody will walk 960 ft every day for her fitness program.

Let's look at another.

Daniel has 25 ft of decorative border for his rectangular bulletin board. If the width of his board is 3 ft and the length of his board is 10 ft, does he have enough border to line the entire board?

To determine if Daniel has enough border, we must calculate the perimeter of his board. Since it's a rectangle, we know that both widths and both lengths will be the same. Therefore, to find the perimeter, we can either add 3 + 3 + 10 + 10 or we can multiply 2 * 3 and 2 * 10 and then add 6 + 20. No matter which method we use, the perimeter of the board is 26 ft. Since Daniel only has 25 ft of border, he does not have enough to line the entire board.

Here's one last example.

Christy is creating a triangular collage of pictures. One side of the collage is 12 in and the other two sides are 18 in. If she wants to frame the collage with ribbon, how much ribbon will she need? And, if the ribbon costs $0.75 per foot, how much will the ribbon cost her?

To determine the amount of ribbon that Christy needs, we must first figure out the perimeter of her collage. To do so, let's add up the length of all the sides of the triangle: 12 + 18 + 18. Simplifying this calculation leaves us with a perimeter of 48. Therefore, Christy needs 48 in. of ribbon to frame her collage.

Now, let's determine the cost. Recalling that 12 in = 1 ft, we can conclude that 48 in = 4 ft. Since the ribbon costs $0.75 per foot, let's multiply 4 * $0.75. Doing so gives a total of $3. In conclusion, Christy will spend $3 on ribbon for her collage.

Solving with Perimeter

In all of these examples, we were given the measure of each side to calculate the perimeter. Now, let's look at how we can use perimeter to find the measure of the sides.

Here's rectangle DOTS, which has a perimeter of 56:

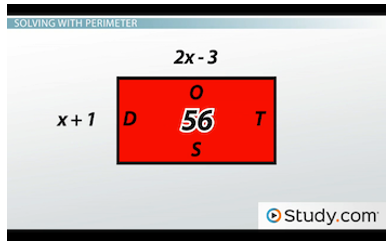
14 -19700468

Rectangle DOTS, with a perimeter of 56

If the length of the rectangle is 2x - 3, and the width of the rectangle is x + 1, how long is the rectangle?

For this problem, knowing the value of x will allow us to determine the length. So, we must first solve for x. Since this is a rectangle, let's multiply the length by two and multiply the width by two. Then, we will add them together to equal the perimeter. This process gives us 2(2x - 3) + 2(x + 1) = 56. From distributing, we get 4x - 6 + 2x + 2 = 56, and after combining like terms, we have 6x - 4 = 56. We must now add 4 to both sides to cancel it out of the equation, leaving us with 6x = 60. Our next step will be to divide each side by 6, giving us x = 10.

Since we were only asked to determine the length of the rectangle, let's plug 10 into the equation for the length, which is 2x - 3. By substitution, we have 2(10) - 3. To calculate, we refer to the order of operations and multiply 2 * 10 before subtracting 3. In the end, the length of rectangle DOTS is 17.

Here's one last example.

Triangle PUD has a perimeter of 162 cm. Side PD is 4 less than twice a number, side PU is 8 less than the number, and side UD is 15 less than three times the number. What is the length of each side of triangle PUD? Since this problem does not directly give us the equation for each side, we will have to create them based on the descriptions.

Triangle PUD, with a perimeter of 162

The length of side PD is 4 less than twice a number. Since we don't know what this number is, we will call it x. So, PD is 4 less than two times x, which means that PD = 2x - 4. Side PU is 8 less than the number, so PU = x - 8, and side UD is 15 less than three times the number, which means that UD = 3x - 15.

We will add all three equations to equal the perimeter. So, our beginning setup is 2x - 4 + x - 8 + 3x - 15 = 162. Combining like terms takes us to 6x - 27 = 162. From here, we cancel out the 27 by adding it to both sides, leaving us with 6x = 189. Then, we will divide each side by 6 to conclude that x = 31.5. We're ready to determine all of the side lengths for triangle PUD.

Substituting 31.5 into each equation, we see that PD = 59 cm, PU = 23.5 cm, and UD = 79.5 cm. To check our work, let's add up all of these lengths. Doing so gives us 59 + 23.5 + 79.5, which is equal to 162. Since this sum is the same as the perimeter we were given, we know that we have correctly solved the problem.

Lesson Summary

In review, perimeter is defined as the distance around an object, shape or figure and is calculated by adding the lengths of all the sides of a polygon. Rectangles have two pairs of congruent sides. The lengths have the same value, and the widths have the same value. This allows us to use addition or a combination of addition and multiplication to calculate the perimeter.

On the other hand, some triangles have congruent sides and some do not; therefore, we should only use addition to calculate the perimeter of triangles. With both shapes, we can also use the perimeter to work backwards and determine the length of each side.

Next Topic

Topics