How to Solve Quadratics That Are Not in Standard Form
It isn't always the case that your equation will be set up nicely for you to solve. In this lesson, learn how to factor or use the quadratic formula to solve quadratic equations, even when they are not in standard form.
Solving Non-Standard Quadratic Equations
You've moved on to level three of Furious Fowls, the game that gives you a mathematical hint but only one chance for you to get your bird to land on the target pig that has your precious eggs. You've gotten here by solving the quadratic hint to find the roots of the equation and predict the place where your bird will land. But here in the third and final level things are going to get pretty tricky. They're going to stop going easy on you by giving you the quadratic all nice and organized, and now the hint will be messy and confusing, but your goal will still be the same: solve the quadratic in order to find the roots and predict where the bird will hit the ground. You ready? Here we go!
Let's line up our shot and get it as close as we think we can... eh, that looks good. What's the hint that it gives us?
-2x (x - 1) + 5 + x = 0
Yikes. Well, it's kind of nice that it equals zero, I guess, but other than that it's pretty much a mess.
Standard Quadratic Form
Both ways we know how to solve quadratics require that the equation is in standard form (y = ax2 + bx + c), and this one definitely is not. But don't let that phase you! Don't panic and think you need to do something crazy. All we need to do is use our algebra skills to move things around and put this equation back into standard form.
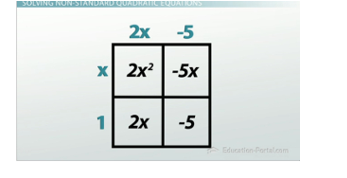
The area method can be used to factor in the first example
Let's start by distributing the -2x to the (x - 1) on the inside of the parentheses in order to change this expression only to addition. Doing that gives us this: -2x2 + 2x + 5 + x = 0, and now it's only a matter of combining like terms to end up with our standard form quadratic, -2x2 + 3x + 5 = 0.
We can now start thinking about solving this, and these numbers aren't too bad, so let's try factoring. This means first factoring out the negative from everything in the trinomial to give us this: -(2x2 - 3x - 5) = 0, and then finding a pair of numbers that have a product of -10 and a sum of -3. Writing out the factors of -10 and looking for the pair that fit our criteria makes it look like -5 and +2 are our winners. That means we can use the area method to factor this out. Substituting those values into the four quadrants and then taking the greatest common factor out of each column and row gives us the factored form of the equation as -(2x - 5)(x + 1) = 0.
The Zero Product Property
That changes the equation in our problem to this: 0 = 2x - 5 or 0 = x + 1, which now allows us to use the zero product property. The zero product property says that any time we multiply two things together and get zero, one of the things we started with must have been zero. That means that in this case either 2x - 5 = 0 or x + 1 = 0. Now it's only a few quick inverse operations to find that our two answers are 5/2 or -1.
x = -1 is a valid solution but doesn't make much sense for our game here. What we want to look at is our 5/2 answer, and it looks like we're a little bit off. We need to get a little more distance. Let's try leveling off our shot and see if that will give us the result you want. Just a little bit lower... okay. But remember, this is the final level, so our new equation probably isn't going to look any nicer than the last one, and sure enough, it's kind of crazy:
2x (3x - 5) = x + 30

The quadratic formula
This one isn't even equal to zero, but that's okay! We still need to do the same thing as earlier - use algebra to change this quadratic back to standard form. First multiplying with the distributive property, then using inverse operations to move everything to the left side of the equation, and finally combining like terms gives us our standard form quadratic equation 6x2 - 11x - 30 = 0.