In the figure, we were given the length of side MO, meaning that we also need the length of side QO for the proportion. But, we were not given this information, so we must calculate it.
To get the length of QO, we must add QP + PO since these two pieces form segment QO. By doing this, we add 7 + 8 to see that QO = 15. Now, we are ready for our proportion.
By going in the same order, our proportion is 7/15 = x/18. Then, when we cross-multiply, we see that 15x = 126. Once we divide both sides by 15, we can conclude that x = 8.4.
Applications of Similar Triangles
Now that we've covered some of the basics, let's do some real-world examples, starting with Sarah and the flagpole. Recall that Sarah is 5 ft. tall and has a 4 ft. shadow, and we are looking for the height of the flagpole, which has a 7 ft. shadow.

Diagram of the triangles formed by Sarah and the flagpole
Do you see the similar triangles above? Sarah and the flagpole are the vertical legs and the shadows are the horizontal legs. Connecting the end of the shadows to the top of Sarah and the flagpole complete the triangles. Since the sun is casting both shadows, and since Sarah is standing right beside the flagpole, the top angles in both triangles are congruent. Additionally, since Sarah and the flagpole are perpendicular with the ground, each triangle has a right angle. Therefore, these triangles are similar by the AA similarity theorem.
Now we can write a proportion. Using x to represent the height of the flagpole, we begin with 5/4 = x/7. After cross-multiplying, we have 4x = 35, and then, by dividing both sides by 4, we see that x = 8.75. Therefore, the flagpole has a height of 8.75 ft.
Let's try another: Julie places a mirror on the ground 30 ft. away from the base of her office building and walks backwards until she can see the top of the building in the mirror. If Julie is 5.5 ft. tall and is standing 5ft. away from the mirror, how tall is the building?
For this scenario, Julie and the building serve as the vertical legs of the triangles and the distances from the mirror to Julie and the building are the horizontal legs. The triangles are completed by connecting the mirror to the top of both Julie and the building.
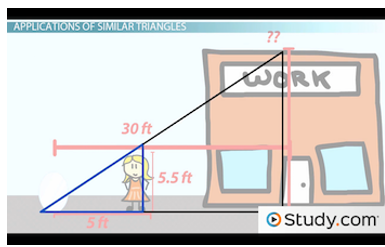
Diagram of the triangles formed by Julie and the building
Since Julie can see the top of her building through the mirror, the two angles formed at the mirror are congruent. Also, Julie and her office building form right angles with the ground, showing us that these two triangles above are also similar by AA. Now, it's time for the proportion.
By letting x represent the height of the building, our beginning proportion is x/30 = 5.5/5. From cross-multiplying, we get 5x = 165. Then, by dividing both sides by 5, we can conclude that x = 33. Therefore, the height of Julie's office building is 33 ft.
Lesson Summary
In conclusion, similar triangles can be applied to solve everyday, real-world problems. Since the triangles are similar, solving with them requires us to set up proportions that compare their corresponding sides. After going in the same order to set up the proportions, cross-multiplying is necessary to complete and solve the problem.