|
There are two important spatial relationships in this question: the relationship
of a sphere and a cube, and the relationship of these two solids to the
crate. Although some might tackle this without any sketching, the visualization
involved is fairly tough, so sketching is a good approach unless you are
very comfortable visualizing solids and calculating volumes.
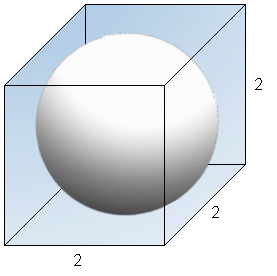
Cube vs. Square: By sketching both solids, we can see that they
would take up equal amounts of space if packed together in a crate. The
sphere, which has a radius of 1 and a diameter of 2, has less volume,
but it takes up the same amount of space due to its shape. This
space is equivalent to the volume of the cube: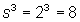 
so each sphere takes up 8 units worth of space.
Solids/Crate: This relationship can be solved via the volume formula
for a rectangle (l × w × h). A rectangle that measures 2 by 4 by 6 holds
2 × 4 × 6 = 48 square units. Once again, this can also be drawn out:
Therefore, each solid, whether a cube or sphere, takes up 8 square units.
Since there are 48 square units of space in the crate, then the crate
can hold a total of 6 solids. The question stem states that there
are 4 cubes in the crate, so there must be at least 2 spheres to fill
the crate. Choice (B) is correct.
|