Angular Position, Displacement, Velocity, and Acceleration
Physics is unlikely to have any questions that simply ask you to
calculate the angular position, displacement, velocity, or acceleration of a
rotating body. However, these concepts form the basis of rotational mechanics,
and the questions you will encounter on
Physics will certainly be
easier if you’re familiar with these fundamentals.
Angular Position
By convention, we measure angles in a circle in a counterclockwise direction
from the positive x-axis. The angular position of a particle is
the angle,
ø,
made between the line connecting that particle to the origin,
O, and the positive x-axis,
measured counterclockwise. Let’s take the example of a point
P on a rotating wheel:
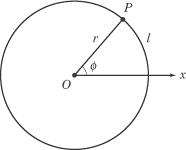
In this figure, point P has an
angular position of
ø.
Note that every point on the line
has the same angular position: the angular position of a point does not depend
on how far that point is from the origin, O.
We can relate the angular position of P
to the length of the arc of the circle between
P and the x-axis by means of an easy equation:
In this equation, l is the length of
the arc, and r is the radius of the
circle.
Angular Displacement
Now imagine that the wheel is rotated so that every point on line
moves from an initial angular position of
øi
to a final angular position of
øf.
The angular displacement,
?,
of line
is:
? = øf - øi
For example, if you rotate a wheel counterclockwise such that the angular
position of line
/changes
from
øi
= 45° = p/4 to
øf
= 135° = 3p/4,
as illustrated below, then the angular displacement of line
is 90° or p/2
radians.
For line
to move in the way described above, every point along the line must rotate
90ºº counterclockwise. By definition, the
particles that make up a rigid body must stay in the same relative position to
one another. As a result, the angular displacement is the same for every point
in a rotating rigid body.
Also note that the angular distance a point has rotated may or may not equal
that point’s angular displacement. For example, if you rotate a record
45º clockwise and then
20º counterclockwise, the angular
displacement of the record is 25º, although
the particles have traveled a total angular distance of
65º. Hopefully, you’ve already had it
hammered into your head that distance and displacement are not the same thing:
well, the same distinction applies with angular distance and angular
displacement.
Angular Velocity
Angular velocity,
?,
is defined as the change in the angular displacement over time. Average angular
velocity,
,
is defined by:
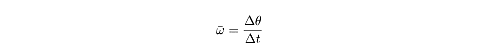
Video Lesson - Angular Velocity
Angular velocity is typically given in units of rad/s. As with angular
displacement, the angular velocity of every point on a rotating object is
identical..
Angular Acceleration
Angular acceleration,a, is defined as the rate of change of angular velocity over time.
erage angular acceleration,
,
is defined by:
Angular acceleration is typically given in units of rad/s2.
v>
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.