Lesson: Chapter - 10

Domain and Range

Several of the Subject Math questions about functions will focus on domain and range. These questions are straightforward if you understand the basic concepts and know what to look for.

Domain

We discussed the concept of a function’s domain earlier in this chapter. The domain of a function is the set of inputs to the function that produce valid outputs. It is common for a domain to include only positive numbers, only negative numbers, or even all numbers except one or two points. As an example of a function that is undefined on a certain interval, consider f(x) = vx. A negative number has no square root defined in the real number system, so f(x) is undefined for all x < 0.

Video Lesson - Domain of a Function

Finding the Domain of a Function

The Math IC may ask you to find the domain of a given function. When you are solving a problem of this sort, you should begin by assuming that the domain is the set of real numbers. The next step is to look for any restrictions on the domain. For example, in the case of f(x) = vx, we must restrict the domain to non-negative numbers since we know that you can’t take the square root of a negative number.

In general, when finding a domain on the Subject Math, there are two main restrictions to be on the lookout for:

1. Division by zero. Division by zero is mathematically impossible. A function is therefore undefined for all the values of x for which division by zero occurs. For example, f(x) = ¹/_{x – 2} is undefined at x = 2, since when x = 2, the function is equal to f(x) = ¹/₀.
2. Even roots. An even root (a square root, fourth root, etc.) of a negative number does not exist. A function is undefined for all values of x that cause a negative number to be the radicand of an even root.

Recognizing that these two situations cause the function to be undefined is the key to finding any restriction on the function’s domain. Once you’ve discovered where the likely problem spots are, you can usually find the values to be eliminated from the domain easily.

By now, you must be itching for a sample problem:

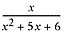
In this question, f(x) has variables in its denominator, which should be a red flag that alerts you to the possibility of division by zero. We may need to restrict the function’s domain to ensure that division by zero does not occur. To find the values of x that cause the denominator to equal zero, set up an equation and factor the quadratic: x² + 5x + 6 = (x + 2)(x + 3) = 0. For x = {–2, –3}, the denominator is zero and f(x) is undefined. Since it is defined for all other real numbers, the domain of f(x) is the set of all real numbers x such that x ? –2, –3. This can also be written as {x: x ? –2, –3}.

Here’s another example:

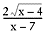
This function has both warning signs: an even root and a variable in the denominator. It’s best to examine each situation separately:

1. The denominator would equal zero if x = 7.
2. The quantity under the square root (the radicand), x – 4, must be greater than or equal to zero in order for the function to be defined. Therefore, x = 4.

The domain of the function is therefore the set of real numbers x such that x = 4, x ? 7.

So far we have looked only at functions that take a single variable as input. Some functions on the test take two variables. For example:

A two-variable function is not very different from the basic single-variable variety you’ve already seen. Essentially, the domain of this function is a set of ordered pairs of real numbers (s, t), rather than a set of single real numbers.

Evaluating such a function follows the same process as evaluating a single-variable function. Just substitute for the variables in the equation and do the algebra. Try to find f(8, 14), using the definition of f(s, t) above.

Piecewise Functions

Not all functions must have the same definition across their entire domain. Some functions have different definitions for different intervals of their domains; this type of function is called a piecewise function. Here is a typical example:

To evaluate a piecewise function, you need to find the correct interval for the given definition and evaluate as usual. For example, what is g(6), using the above piecewise definition of g(x)?

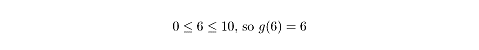
Range

A function’s range is the set of all values of f(x) that can be generated by the function. In general, the range for most functions whose domain is unrestricted is the set of all real numbers. To visualize the concept of range, consider two trigonometric functions, sin x and tan x.

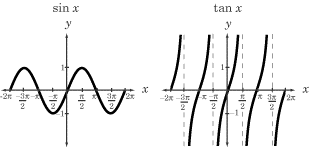
What values of the y-axis are reached on each graph? On the graph of tan x, you can see that every possible value of y, from negative infinity to positive infinity, is included in the range. The range could be written as {y: –8 = y = 8}. Contrast this with the graph of sin x, in which the range is quite limited. You’ll notice that only the values between –1 and 1 are part of the range. We’ll write the range using another common notation: {–1 = f(x) = 1}.

Of course, there are other ways that a function’s range might be limited. For example, if a function has a limited domain (only certain x values are allowed), its range might be limited as well. In addition, there are two main reasons that a function’s range would be restricted:

Absolute value.

Remember that by definition, the absolute value of a quantity is always positive. So, in a simple case, f(x) = |x|, you know that f(x) must always be positive, and so the range excludes all negative numbers. Be careful, though, not to assume that any function with an absolute value symbol has the same range. For example, the range of g(x) = –|x| is {y: –8 = y = 0} and the range of h(x) = 10 + |x| is {10 = h(x) = 8}.

Even exponents.

Any time you square a number (or raise it to any multiple of 2) the resulting quantity will be positive. As in the case of the absolute value, though, don’t assume that the range will always be {y: 0 = y = 8}.

Determining the range of a complex function is similar to finding the domain. First look for absolute values, even exponents, or other reasons that the range would be restricted. Then simply adjust that range step by step as you complete the questions. The best way to get the hang of it is to practice.

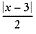
The absolute value around |x – 3| tells us that the range for that term excludes negative numbers (y: 0 = y = 8). |x – 3| is then divided by 2, so we must also divide the range by 2: (y: ⁰/₂ = y = ⁸/₂). Obviously, this doesn’t change the range, since both zero and infinity remain unchanged when halved. Now for a more complicated example:

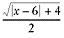
Let’s tackle this example step by step.

1. The absolute value restricts the range to {0 = f(x) = 8}.
2. Add 4 to each bound of the range. This action affects only the lower bound: {4 = f(x) = 8}.
3. Taking the square root again only affects the lower bound: {2 = f(x) = 8}.
4. Finally, divide the bounds of the range in half to determine the range of the entire function: {1 = f(x) = 8}.

Note that addition, subtraction, multiplication, division, and other mathematical operations cannot affect infinity. That’s why it is particularly important that you look for absolute values and even roots. Once you can find a bound on a range, then you know that the operations on the function will affect that range.

Before we move on, here is one last example that uses a slightly different range notation that you might come across on the Math IC:

Once again, take a step by step approach to finding the range:

1. The range of f(x) – x² is {0, 8}.
2. The range of f(x) –³/₂ x² is {–8, 0}.
3. The range of f(x) –³/₂ x² + 2 is therefore {–8, 2}, or simply {f(x) = 2}.

Video Lesson - Range of a Function

The Range of a Function with a Prescribed Domain

Occasionally the Math IC will present you with a question in which the domain of a function is restricted to a given interval, and you are asked to find the range of the newly restricted function. For example:

f(x) = 2x² + 4 for –3 < x < 5. What is the range of f?

The best way to solve this type of problem is to manipulate the domain of x in exactly the same way that x is manipulated in the function. First x is squared, then multiplied by 2, then added to 4; we simply need to do the same operations to the bounds of the domain:

1. –3 < x < 5
2. 0 < x² < 25
3. 0 < 2x² < 50
4. 4 < 2x² + 4 < 54

The range of f(x) is {4 < f(x) < 54}.

Next to display next topic in the chapter.

Mathematics Practice Questions