Lesson: Chapter - 10
Inverse Functions
The inverse of a function “undoes” that function. An example may be the best way
to explain what this means: the inverse of x2 is vx.
Let’s see how vx “undoes” x2:
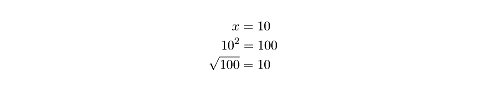
For the Math IC, it is important to know how to find the inverse of a simple
function mathematically. For example:
What is the inverse of
f(
x) = 3
x + 2?
Video Lesson - Inverse of a Function
The easiest way to find the inverse of a function is to break the function apart
step by step. The function f(x) = 3x + 2 requires that for
any value of x, it must be first multiplied by three and then added to 2.
The inverse of this function must begin by subtracting 2 and then dividing by
three, undoing the original function: f–1(x) =
x–2/3.
div>
You should know how an inverse works in order to deal with any conceptual
inverse questions the Math IC might throw at you. But if you are ever asked to
come up with the inverse of a particular function, there is an easy method that
will always work.
- Replace the variable f(x) with y.
- Switch the places of x and y.
- Solve for y.
- Replace y with f–1(x).
Here’s an example of the method in action:
What is the inverse of the function
f(
x) =
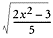
?
First, replace f(x) with y. Then switch the places of x
and y, and solve for y.
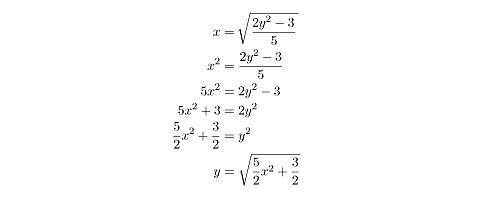
.gif)
Finding Whether the Inverse of a Function Is a Function
Contrary to their name, inverse functions are not necessarily functions at all.
Take a look at this question:
Is the inverse of
f(
x) =
x3 a function?
Begin by writing y = x3. Next, switch the places of
x and y: x = y3. Solve for y: y
= 3vx.Now you need to analyze the inverse of the function and decide whether for every
x, there is only one y. If only one y is associated with
each x, you’ve got a function. Otherwise, you don’t. In this case, every
x value that falls within the domain X = 0 turns out one value for y, so f–1(x)
is a function.
Here’s another question:
What is the inverse of
f(
x) = 2|
x – 1|, and is it a function?
Again, replace x with y and solve for y:

Now, since you’re dealing with an absolute value, split the equations:
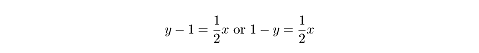
Therefore,

The inverse of f(x) is this set of two equations. As you can see,
for every value of x except 0, the inverse of the function assigns two
values of y. Consequently, f–1(x) is not a
function.
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.