How to Solve Exponential Equations

How to Solve Exponential Equations

If you're planning on putting some money in the bank to save up for that next thing you've got to have, it might be best to know a little about exponential equations first. Learn how to check how long it will take you to have as much money as you need here!

Exponential Equations in the Real World

One of the most likely places for you to find an exponential equation in real life (and also on a standardized test) is in a bank when you're talking about saving money. When you are letting your money gain interest, chances are it's gaining interest exponentially. For example, every year you keep it in the bank, it grows 5% more. One equation that is often used to calculate how fast your money will grow is this: A=Pert

Calculating how fast your money in the bank will grow is an example of an exponential equation

It can help us say things like, if you put $500 in a bank account that pays 6% interest, after 10 years, your money will have turned into $911. But if instead I wanted to know how long it would take for that $500 to become enough for the $4,000 motorcycle I've had my eye on, I'd be stuck with an exponential equation that needed solving.

How to Solve an Exponential Equation

Substituting the variables in the correct places in the equation would this time give me 4,000=500e0.06(t). The goal is to figure out what is t, or how many years it is going to take for the initial $500 to turn into the $4,000 I want it to be. I simply have to use inverse operations to undo things one at a time to try to get the t by itself. I undo multiplication with division, and I end up with this equation: 8=e0.06(t). But now we have to undo an exponential. The variable I'm trying to solve is stuck in the exponent,

Good thing we know about logs. In order to undo the base of an e, I have to take the log with the base of an e, and the log with the base of an e is called the natural log. So by taking the natural log of both sides, the natural log of e cancels out, or undoes, and I just get the 0.06(t). On the other side I have the natural log of 8.

Because the ln button is on my calculator, I don't have to use the change of base formula to evaluate it, and we can just plug it in to find that it equals about 2.079. Now I simply have to undo one more multiplication step with division, and I find that t would have to be about 34.66 years. I've got a ways to go.

Using the Change of Base Formula

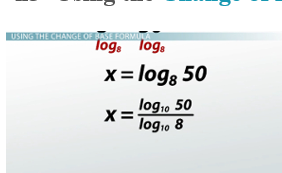
Use the change of base formula to undo exponentials that are not commonly found on a calculator

As a quick note, when we use logs to undo exponentials that aren't the common ones on our calculator, say, undoing 8x = 50 with the log base 8 on both sides, we need to use the change of base formula to estimate our answer. So the log base 8 on the left cancels with the 8x, and we just get x, but on the right I have the log base 8(50). Because the log base 8 isn't a very common logarithm, it's not on our calculator, so we have to use the change of base formula. The change of base formula says I can turn the log base 8 into log base 10s being divided by each other. So I get the log base 10 (50) divided by the log base 10 (8), which I can plug into my calculator to find is about 1.88.

Solving With Similar Bases

We can also solve exponential equations that have exponentials on both sides, like this: 5(2x - 1) = 5(3x + 5). Because I have variables stuck in exponents on either side, I would like to undo the exponential on both sides. Luckily, the base on both sides is 5, so they can be undone the same way. By taking the log base 5 of both sides, they both cancel out, and I simply get 2x - 1 = 3x + 5. Now this is just a matter of using the skills we learned way back in the linearity section to undo addition and division and subtraction, and we eventually end up with that x = -6.

Solving With Different Bases

But sometimes the problems will not be as straightforward and will make you do some work before you can bust out the log. Take this one: (1/8)(6x + 2) = 4(6x + 12).

Make bases the same so it is easier to solve problems with different bases

Again, I have variables stuck in exponents on both sides, so I'd like to undo the exponentials on both sides. But because the bases are different, taking, for example, the log base 4 of both sides would only cancel out the right. On the left I would have a pretty messy log that I'd rather not deal with. So in order to have both bases go away - both exponentials go away - I need both bases to be the same.

Luckily 1/8 and 4 can both be rewritten as powers of 2. By remembering that negative exponents give us fractions, I can say that 1/8 is the same thing as 2-3. I can also say that 4 is 22, and now I have the base of my exponentials the same. I do have to use the power of a power property to multiply exponents together when they are raising each other, which leaves me with the equation 2(-18x - 6) = 2(12x + 24). Now that both bases are the same, this problem is just like the previous one. I can take the log base 2 of both sides, both bases magically disappear, and I simply get -18x - 6 = 12x + 24. Again, we solve with the inverse operations that we've hopefully known for a while now, undoing subtraction with addition, undoing addition with subtraction, undoing multiplying with dividing, and we find out that x must have been -1.

Lesson Summary

To review, exponential equations often appear when dealing with interest and money and can be solved by using logarithms.

When you have two exponentials that don't have the same base, try to rewrite them as the same number so that you can use the same log to cancel both of them out.

We can also solve exponential equations with exponentials on both sides of the equation, but remember that when the bases of those exponentials aren't the same, you'll have to first make them the same before you can undo them with a log.