
If we can find what terms must have been on the outside of this chart to get multiplied in and give us what we have here, we'll be done. We do this by dividing out the greatest common factor from each row and column of our chart. So, if I look at the top row of this chart, I have a 2x2 and -6x. I need to ask myself what do those things have in common? Well, 2 and 6 are both divisible by 2, so I can take out a 2. But they also both have an x, which means I also take out an x, so I can pull a 2x to the outside of that row. Going down a row to the bottom, 1x and -3, they don't have any factors with the numbers in common, and they also don't have any variables in common, which means the only thing I can divide out is a 1. Now, we go to the columns. Let's start in the left column, 2x2 and 1x. The numbers don't have anything in common but the variables do, which means I can take out 1x. Finally, the column on the right: -6x and -3. Both share a -3, which means I divide that out and write it on top. What we now have on the left and above our little area model is our factored answer. The terms that are on the same side are the terms that go in parentheses together to make up our two binomials, and I end up with (2x + 1)(x - 3). You can always quickly multiply out your answer to make sure you got the right thing, and if you do that here, looks like we're good.
Factoring quadratics like this take a while, and they're not always simple, so practice is key. Let's do one more example during this lesson.
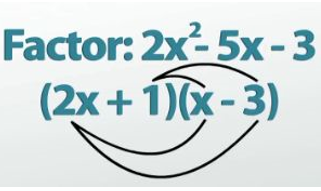
Multiply the answer to make certain it is correct.
nother Example
Factor 9x2 - 4.
To unlock this lesson you must be a Study.com Member. Create your account
Register for a free trial
Are you a student or a teacher?
I am a student I am a teacher
You are viewing lesson 6 in chapter 9 of the course:
GMAT Prep: Help and Review
24 chapters | 272 lessons
Ch
Basic Arithmetic Calculations
: Help...
Rational Numbers
: Help and...
Decimals and Percents
: Help and...
Data & Statistics
: Help and...
Basic Algebraic Expressions
: Help and...
Exponents
: Help and Review- Algebraic Linear Equations &...
Ch - Algebra - Absolute Value Equations &...
Ch
Algebra - Polynomials
: Help and Review