SAT Math Multiple Choice Questions

In this lesson, we'll look at multiple choice questions on the SAT math section. We'll practice with some example questions, and cover tips and tricks for how to do well on this type of question.

Multiple Choice Questions

Antony is worried about the math portion of the SAT. He's just not sure what to expect, or how to prepare. What types of questions are there? What should he do on test day to help?

Most of the questions on the math section of the SAT are multiple choice questions, which offer four possible answer choices. Antony will have to choose the best answer from those four choices. Antony will also see other questions on the test, called grid-in questions, but for now, let's help Antony prepare by looking closer at multiple choice questions, including practicing with some examples and figuring out some test-taking strategies he can use on the day of the exam.

Practice

Let's start Antony off with a simple, straightforward example, just to get him used to multiple choice questions. Ready? Here we go!

1. (3x - 4) / 2 = 2.5, so x =

1. 2
2. 3
3. 4
4. 5

That's pretty straightforward. All Antony has to do is solve for x. First, he multiplies both sides by 2, which gives him: 3x - 4 = 5. Then, he adds 4 to both sides to get 3x = 9. Now it's looking pretty easy! He divides both sides by 3, which gives him x = 3. He looks down at the answer choices, and he can see that answer choice (b) is 3, so that's the correct answer.

Ok, now that Antony's warmed up, let's look at a more complex problem that he might see on the test.

That takes a little more thought, because it's not quite as straightforward. But when Antony thinks about it, he realizes that the answer is (d).

Let's look at another example, one that involves a graph. Many questions on the math portion of the SAT include graphics, like graphs or charts or tables, with them. Check this one out:

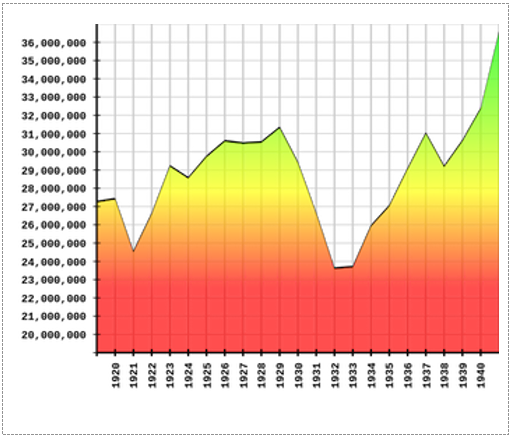
2. This graph shows the U.S. employment rate between 1920 and 1940. According to this graph, between 1920 and 1940, how many times did the employment rate increase by at least 1,000,000 in a single year?

1. 5
2. 6
3. 8
4. 9

Oh, boy. This doesn't involve calculations, but it does involve really studying the graph. Antony notices that each horizontal line represents 1,000,000, and that every vertical line represents a year. So he's looking for boxes where the employment rate line moves all the way up, from one horizontal line to another. For example, look between 1933 and 1934. Antony can see how that year, the employment rate went up by at least 1,000,000.

Antony looks at the graph and notices several times that the employment rate increased by at least 1,000,000 in a single year. For example, he counts 1921-22, 1922-23, and (as we've seen) 1933-34. He also counts 1934-35, 1935-36, 1936-37, 1938-39, and 1939-1940. Altogether, Antony has counted eight years that the employment rate increased by at least 1,000,000. When he looks at the answer choices, he realizes that answer choice (c) is 8, so he marks that one.

Tips and Strategies

Antony's starting to get the swing of things. He can see how multiple choice questions are formatted and the variety of questions that he might see on the test. But, how can he maximize his time and brainpower to do well on the test? What tips and strategies should he employ?

Some tips are true of all multiple choice questions. For example, there is no penalty for getting an answer wrong, so Antony should guess if he's not sure of the answer. In addition, sometimes it's easy to eliminate wrong answer choices. For example, in the question about Lulu figuring out how many hours she should work to make at least $500, answer choice (c) includes the less than or equal to sign. Lulu doesn't want to make less than $500, so Antony can immediately eliminate that answer choice. Then, if he has to guess, he can choose one of the other choices.

Some strategies, though, are specific to some types of questions. For example, let's look back at the first question Antony solved before. In this question, Antony is asked to solve an equation. For questions like this one, Antony can plug in the answer choices to find the right one. For example, answer choice (a) is 2. If Antony plugs 2 into the equation, he gets (3 * 2 - 4) / 2 = 2.5. Now all he has to do is the math.

Clearly, this is not the right answer choice, because 1 does not equal 2.5. But, remember he chose answer (b). He can check his answer by plugging 3 into the equation. When he does, he gets (3* 3 - 4) / 2 = 2.5. Again, all he has to do now is the math. That works out correctly, so Antony knows that he's chosen well.

Another good tip for questions that ask you to solve equations is to show all your work so that you can check for errors later. Antony has written down his work as he's solved the equation, so if he accidentally wrote that 5 / 2 equals 2 instead of 2.5, he can easily see where he made his mistake.

With graphs and charts, a good tip is to draw on the graphics to help you organize your information. Remember the graph where Antony had to count the number of years that the employment rate increased by at least 1,000,000. Antony can help himself keep track by putting an 'x' or check mark in each box that he counts.