Polynomials Functions: Exponentials and Simplifying

Polynomials Functions: Exponentials and Simplifying

How do we keep track of a rapidly multiplying population of bunnies? Well, those are simply powers of 2. Review powers and simplify problems with exponents in this lesson.

Bunnies Galore

Have you ever heard of that bunny problem? You know, the one where you start out with one bunny, and then all of a sudden you have two bunnies, and each of those bunnies has a bunny, so you end up with four bunnies? Each of those bunnies has a bunny, and you have eight bunnies and then 16 and 32 and 64 - your population just keeps growing!

x to the nth Power

You could've said that your population started out with one times two bunnies times two bunnies times two bunnies and so on and so forth. If we ignore that one, because it doesn't really matter in this case, you end up with a case of repeated multiplication: 2 * 2 * 2 * 2 * 2 ... When x=2, we can write this as x * x * x * x * x ... and so on and so forth, which gives us x^n. Now, in x^n, x is the base, n is the exponent, and we call this x to the nth power. In the case of our population, we had 2 * 2 * 2 * 2 * 2, and let's just cap it off there. So we have five 2's for a population of 2^5.

Example of x to the nth power

Powers in Daily Life

Now these powers are used all over in math and really all over the world. For example, if we want to look at mummies and know how old they are, we use an approach like carbon dating. And, carbon dating is used with powers, which might be something like 2.7^-t, where t is time. So we're using a power to determine the age of a mummy. Another example is the metric system. In the metric system, we're using powers that look like 10^x meters. Now, if x=-10, you're looking at something about the size of an atom. If x=20, you're looking at something roughly the size of the galaxy.

Polynomials

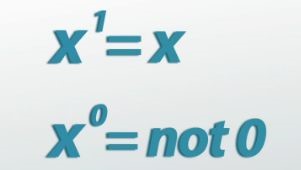
Properties of x to the n

Properties of Polynomials

So what are the properties?

Addition Property

There are no addition properties; there's nothing special for addition. For example 2^3 + 2^2 does NOT equal 2^5. You can see this because 2^3 = 8 and 2^2 = 4 while 2^5 = 32, and 8 + 4 = 12, not 32.

Multiplication Property

Now, for multiplication, we do have some properties, like x^3 * x^2. Well, x^3 = x * x * x and x^2 = x * x. So we know that when we multiply those together, it will equal x * x * x * x * x, which is x^5. So for multiplication, (x^3)(x^2) = x^5. You can generalize that to (x^n)(x^m)=x^(n + m). Going back to the case of 2, we have 2^3 * 2^2 = 8 * 4 = 32 = 2^5.

Division Property

What about division? Well, if I have 1 / (x^2), I can write that as x^-2. This one's a little but funky, but it's a useful notation. You can use it in combination with multiplication to find things like (2^3) / (2^2). If you solve this out, you have 8 / 4. We can also think of it as (2^3)(2^-2), because 1 / (2^2) is 2^-2. Then, I can use my multiplication property and say this is equal to 2^(3 - 2), where I've added my exponents of 3 and -2. So, 2^(3 - 2) = 2^1 = 8 / 4 = 2.

Powers Property

Our last property is that of a power. Say we have (2^2)^3. This is that same as saying (2 * 2)(2 * 2)(2 * 2), which is 2^6. It's reasonable to think that (2^2)^3 is the same as saying 2^(2 * 3), which is equal to 2^6. Again, you can generalize that by saying (x^n)^m = x^(n*m).

This is the same as saying (2x2) (2x2) (2x2).

Lesson Summary

We looked at repeated multiplications, or our bunny problem, and we can write those as x^n, where x is the base and n is the exponent, which is called x to the nth power. We know for these that there are no addition rules, but there are multiplication, division and power rules. There's also that funny property where x^0=1.