2) Combined Work
a) If 'A' and 'B' can finish the work in 'x' & 'y' days respectively, then
A's one day work = 1/x
B's one day work = 1/y
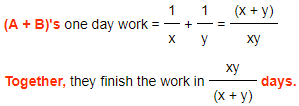
b)If 'A', 'B' & 'C' can complete the work in x, y & z days respectively, then
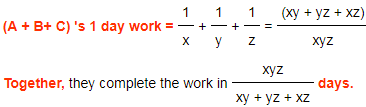
c) If A can do a work in 'x' days and if the same amount of work is done by A & B together in 'y' days, then
A's one day work = 1/x
(A+B)'s one day work = 1/y

d) If A & B together perform some part of work in 'x' days, B & C together perform it in 'y' days and C & A together perform it in 'z' days, then
(A + B)'s one day work = 1/x
(B + C)'s one day work = 1/y
(C + A)'s one day work = 1/z
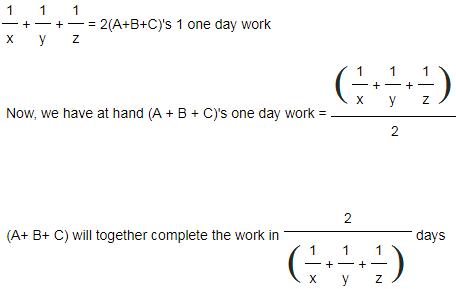
If A works alone, then deduct A's work from the total work of B & C to find the time taken by A alone.
For A working alone, time required =A's work - (A+B+C)'s combined work
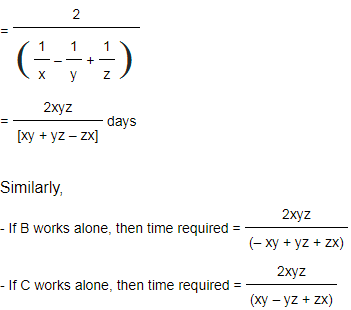
3) Man -Work -Hour related problems
Remember that M D H/ W= Constant
where,
M: Number of Men
D: Number of Days
H: Number of Hours
W: Amount of Work done
If men are fixed, work is proportional to time. If work is fixed , time is inversely proportional to men. Thus,
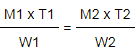
Once you have understood the following simple things, this chapter will become extremely easy for you.
a) Work and time are directly proportional to each other
b) Number of men and time are inversely proportional to each other
c) And, work can be divided into equal parts i.e. if a task is finished in 10 days, in one day you will finish (1/10th) part of the work.