|
|
This problem , like the last one, asks us to find a maximum distance,
but this time we're dealing with a solid figure that is a bit more difficult
to visualize. Drawing a solid figure with the given dimensions is a good
idea:
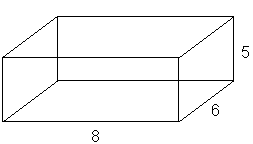
Now, what is the question asking us to find? The longest possible straight
line between any two points on the box. Using our diagram as a guide,
we can see that the diagonal of the 8 by 6 side of the rectangle might
be the longest distance, but remember that we are now dealing with a solid;
the inside of the rectangle must now be considered as well. By sketching
on our diagram, we find that the longest distance is actually the inside,
3-D diagonal as shown below:
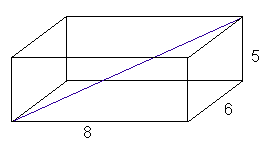
This line is the hypotenuse
of the height of the box and of the diagonal
of the 8 by 6 box side
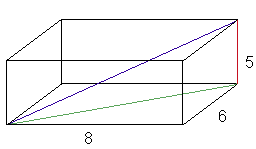
Since the 8 by 6 diagonal is the hypotenuse
of a triangle with legs of 6 and 8, then the diagonal
must equal 10 (common right triangle 6:8:10). We can then use the Pythagorean
theorem to find the length of the blue line, which is the maximum distance:
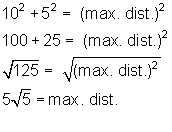
Choice (B) is correct. As you can see, it would be very difficult to keep
all of that straight without a sketch.
|