2.B
The area under a force vs. time graph tells us the impulse given to the rock.
Since the rock is motionless at t = 0,
the impulse given to the rock is equal to the rock’s total momentum. The area
under the graph is a triangle of height 50
N and length 4max s:
P = 1/2(50N)(4 s) = 100 kg. m/s
Calculating the rock’s velocity, then, is simply a matter of dividing its
momentum by its mass:
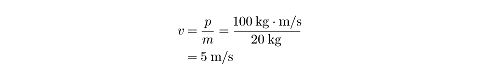
3.D
This is a conservation of momentum problem. The initial momentum of the system
must be equal to the final momentum. The initial momentum of the system is:
P = mv = (60 kg + 20 kg)(7m/s) = 560 kg . m/s
The final momentum of the system is the sum of the momentum of the box and of
the skateboarder. Since the box is thrown in the opposite direction of the
skateboard’s initial momentum, it will have a negative momentum. Because the
final momentum and the initial momentum are equal, we know that the final
momentum of the skateboarder minus the momentum of the box will equal
560max kg · m/s. With this information, we can
solve for vmax, the skateboarder’s
final velocity:
4.D
The law of conservation of linear momentum tells us that the
xmax-component of the system’s momentum
must be equal before and after the collision. The
xmax-component of the system’s momentum before the collision is the
momentum of the large disc. The xmax-component
of the system’s momentum after the collision is the
xmax-component of the momentum of both
of the smaller discs put together. Since momentum is
pmax =
mvmax, and since the larger disc
has twice the mass of the two smaller discs put together, that means that the
velocity of the two smaller discs must be twice the velocity of the larger disc;
that is, 50max m/s.
5.D
We have equations for kinetic energy, KE
max=
1/2
mvmax2, and momentum, p =
mvmax, both of which include variables for mass and velocity. If we
first solve for velocity, we can then plug that value into the equation and
solve for mass:
If vmax =
4max m/s, then we can plug this value into the equation for momentum to find
that pmax =
4mmax =
50max kg · m/s, and conclude that mmax
= 12.5max kg.
6.B
The law of conservation of momentum tells us that the initial momentum of the
system is equal to the final momentum of the system. The initial momentum is
p = mvmax, and the final momentum is
,
where
is the final velocity of the two objects. Knowing that
,
we can solve for
:
7.E
Momentum is conserved in this collision. If the mass is moving with velocity
vmax before impact and the two-mass
system is moving with velocity
after impact, we know that
>.
We also know that the kinetic energy of the two-body system is
E max=
1/2max
.
If we solve for
,
we find:
From the equation
,
we can conclude that the initial velocity of the first body,
vmax, is double
.
If the value for
is given in terms of KEmax in the
equation above, then the value of vmax
is simply twice that,
.
8.C
Impulse is defined as the change in momentum. Since the hockey puck is initially
at rest, its change in momentum is simply its momentum after it has been set in
motion. In other words, the momentum of the puck in motion is equal to
Jmax.
When the puck collides with the other object, momentum is conserved, so the
system of the puck and the other object also has a momentum of
Jmax. This momentum is equal to the
mass, m + Mmax, of the system,
multiplied by the velocity of the two-body system,
v'.
Solving for
v'
is now quite easy:
v.gif)
9.B
The velocity of the center of mass of the system is the same as the total
velocity of the system. To find the total velocity of the system, we need to
find the total momentum of the system and divide it by the total mass of the
system.
The momentum of the first mass is P1
= 10max kg · m/s to the right, and the
momentum of the second mass is P2
= 20max kg · m/s to the left. Therefore, the
total momentum of the system isP 1 + P2 = 10max kg · m/s to the left. Since the total
mass of the system is 2max kg, we can find the
total velocity of the system by dividing its momentum by its mass:
10.D
The only energy in the system is the kinetic energy of the two masses. These can
be determined through two easy calculations:
Back
Next
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.