Lesson: Chapter - 9

Center of Mass

When calculating trajectories and collisions, it’s convenient to treat extended bodies, such as boxes and balls, as point masses. That way, we don’t need to worry about the shape of an object, but can still take into account its mass and trajectory. This is basically what we do with free-body diagrams. We can treat objects, and even systems, as point masses, even if they have very strange shapes or are rotating in complex ways. We can make this simplification because there is always a point in the object or system that has the same trajectory as the object or system as a whole would have if all its mass were concentrated in that point. That point is called the object’s or system’s center of mass.

Video Lesson -

Consider the trajectory of a diver jumping into the water. The diver’s trajectory can be broken down into the translational movement of his center of mass, and the rotation of the rest of his body about that center of mass.

A human being’s center of mass is located somewhere around the pelvic area. We see here that, though the diver’s head and feet and arms can rotate and move gracefully in space, the center of mass in his pelvic area follows the inevitable parabolic trajectory of a body moving under the influence of gravity. If we wanted to represent the diver as a point mass, this is the point we would choose.

Our example suggests that Newton’s Second Law can be rewritten in terms of the motion of the center of mass:

F_net = ma_cm

Put in this form, the Second Law states that the net force acting on a system, F_net, is equal to the product of the total mass of the system, M, and the acceleration of the center of mass, a_cm. Note that if the net force acting on a system is zero, then the center of mass does not accelerate.

Similarly, the equation for linear momentum can be written in terms of the velocity of the center of mass:

p = mv_cm

You will probably never need to plug numbers into these formulas for subject test Physics, but it’s important to understand the principle: the rules of dynamics and momentum apply to systems as a whole just as they do to bodies.

Calculating the Center of Mass

The center of mass of an object of uniform density is the body’s geometric center. Note that the center of mass does not need to be located within the object itself. For example, the center of mass of a donut is in the center of its hole.

For a System of Two Particles

For a collection of particles, the center of mass can be found as follows. Consider two particles of mass m₁ and m₂ separated by a distance d:

If you choose a coordinate system such that both particles fall on the x-axis, the center of mass of this system, x_cm, is defined by:

For a System in One Dimension

We can generalize this definition of the center of mass for a system of n particles on a line. Let the positions of these particles be x₁, x₂,........x_n. To simplify our notation, let M be the total mass of all n particles in the system, meaning M = m₁ + m₂ + ........... + m_n. Then, the center of mass is defined by:

For a System in Two Dimensions

Defining the center of mass for a two-dimensional system is just a matter of reducing each particle in the system to its x- and y-components. Consider a system of n particles in a random arrangement of x-coordinates x₁, x₂,........x_n and y-coordinates y₁,y₂,........y_n. The x-coordinate of the center of mass is given in the equation above, while the y-coordinate of the center of mass is:

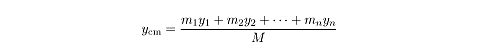
How Systems Will Be Tested on subject test Physics

The formulas we give here for systems in one and two dimensions are general formulas to help you understand the principle by which the center of mass is determined. Rest assured that for subject test Physics, you’ll never have to plug in numbers for mass and position for a system of several particles. However, your understanding of center of mass may be tested in less mathematically rigorous ways.

For instance, you may be shown a system of two or three particles and asked explicitly to determine the center of mass for the system, either mathematically or graphically. Another example, which we treat below, is that of a system consisting of two parts, where one part moves relative to the other. In this cases, it is important to remember that the center of mass of the system as a whole doesn’t move.

Example

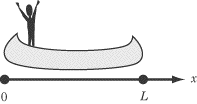
A fisherman stands at the back of a perfectly symmetrical boat of length L. The boat is at rest in the middle of a perfectly still and peaceful lake, and the fisherman has a mass ¹/₄ that of the boat. If the fisherman walks to the front of the boat, by how much is the boat displaced?

If you’ve ever tried to walk from one end of a small boat to the other, you may have noticed that the boat moves backward as you move forward. That’s because there are no external forces acting on the system, so the system as a whole experiences no net force. If we recall the equation F_net = ma_cm, the center of mass of the system cannot move if there is no net force acting on the system. The fisherman can move, the boat can move, but the system as a whole must maintain the same center of mass. Thus, as the fisherman moves forward, the boat must move backward to compensate for his movement.

Because the boat is symmetrical, we know that the center of mass of the boat is at its geometrical center, at x = ^L/₂. Bearing this in mind, we can calculate the center of mass of the system containing the fisherman and the boat:

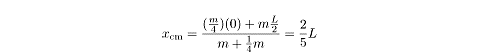
Now let’s calculate where the center of mass of the fisherman-boat system is relative to the boat after the fisherman has moved to the front. We know that the center of mass of the fisherman-boat system hasn’t moved relative to the water, so its displacement with respect to the boat represents how much the boat has been displaced with respect to the water.

In the figure below, the center of mass of the boat is marked by a dot, while the center of mass of the fisherman-boat system is marked by an x.

At the front end of the boat, the fisherman is now at position L, so the center of mass of the fisherman-boat system relative to the boat is

The center of mass of the system is now ³ /₅ from the back of the boat. But we know the center of mass hasn’t moved, which means the boat has moved backward a distance of ¹/₅ L, so that the point ³/ ₅ L is now located where the point ² /₅ L was before the fisherman began to move

Next to display next topic in the chapter.