Lesson: Chapter - 4

Vector Components

As we have seen, vector addition and scalar multiplication can produce new vectors out of old ones. For instance, we produce the vector A + B by adding the two vectors A and B. Of course, there is nothing that makes A + B at all distinct as a vector from A or B: all three have magnitudes and directions. And just as A + B can be construed as the sum of two other vectors, so can A and B. In problems involving vector addition, it’s often convenient to break a vector down into two components, that is, two vectors whose sum is the vector in question.

Basis Vectors

We often graph vectors in an xy-coordinate system, where we can talk about vectors in purely numerical terms. For instance, the vector (3,4) is the vector whose tail is at the origin and whose tip is at the point (3,4) on the coordinate plane. From this coordinate, you can use the Pythagorean Theorem to calculate that the vector’s magnitude is 5 and trigonometry to calculate that its direction is about 53.1º above the x-axis.

Two vectors of particular note are (1,0), the vector of magnitude 1 that points along the x-axis, and (0,1), the vector of magnitude 1 that points along the y-axis. These are called the basis vectors and are written with the special hat notation: 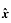and 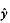respectively.

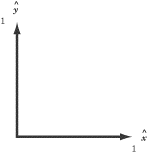
The basis vectors are important because you can express any vector in terms of the sum of multiples of the two basis vectors. For instance, the vector (3,4) that we discussed above—call it A—can be expressed as the vector sum .

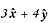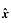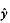The vector3 is called the “x-component” of A and the 4 is called the “y-component” of A. In this site, we will use subscripts to denote vector components. For example, the x-component of A is A_x and the y-component of vector A is A_y .

The direction of a vector can be expressed in terms of the angle ? by which it is rotated counterclockwise from the x-axis.

Vector Decomposition

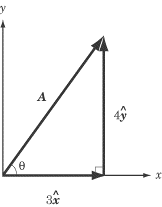
The process of finding a vector’s components is known as “resolving,” “decomposing,” or “breaking down” a vector. Let’s take the example, illustrated above, of a vector, A, with a magnitude of A and a direction ? above the x-axis. Because A_x ,A_y and A form a right triangle, we can use trigonometry to solve this problem. Applying the trigonometric definitions of cosine and sine,

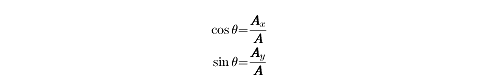
we find:

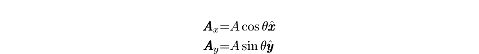
Vector Addition Using Components

Vector decomposition is particularly useful when you’re called upon to add two vectors that are neither parallel nor perpendicular. In such a case, you will want to resolve one vector into components that run parallel and perpendicular to the other vector.

Example

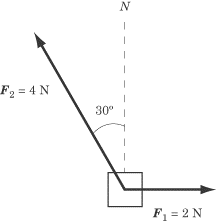
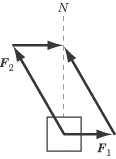
Two ropes are tied to a box on a frictionless surface. One rope pulls due east with a force of 2.0N. The second rope pulls with a force of 4.0N at an angle 30º west of north, as shown in the diagram. What is the total force acting on the box?

To solve this problem, we need to resolve the force on the second rope into its northward and westward components.

Because the force is directed 30° west of north, its northward component is

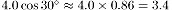
and its westward component is

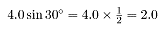
Since the eastward component is also 2.0N, the eastward and westward components cancel one another out. The resultant force is directed due north, with a force of approximately 3.4N.

approximately 3.4N. You can justify this answer by using the parallelogram method. If you fill out the half-completed parallelogram formed by the two vectors in the diagram above, you will find that the opposite corner of the parallelogram is directly above the corner made by the tails of those two vectors.

Next to display next topic in the chapter.