Lesson: Chapter - 18

Optical Instruments

The reflection and refraction we’ve dealt with so far have focused only on light interacting with flat surfaces. Lenses and curved mirrors are optical instruments designed to focus light in predictable ways. While light striking a curved surface is more complicated than the flat surfaces we’ve looked at already, the principle is the same. Any given light ray only strikes an infinitesimally small portion of the lens or mirror, and this small portion taken by itself is roughly flat. As a result, we can still think of the normal as the line perpendicular to the tangent plane.

The four basic kinds of optical instruments—the only instruments that will be tested on
Physics—are concave mirrors, convex mirrors, convex (or converging) lenses, and concave (or diverging) lenses. If you have trouble remembering the difference between concave and convex, remember that, like caves, concave mirrors and lenses curve inward. Convex lenses and mirrors bulge outward.

General Features of Mirrors and Lenses

Much of the vocabulary we deal with is the same for all four kinds of optical instruments. Before we look at the peculiarities of each, let’s look at some of the features they all share in common.

The diagram above shows a “ray tracing” image of a concave mirror, showing how a sample ray of light bounces off it. Though we will take this image as an example, the same principles and vocabulary apply to convex mirrors and to lenses as well.

The principal axis of a mirror or lens is a normal that typically runs through the center of the mirror or lens. The vertex, represented by V in the diagram, is the point where the principal axis intersects the mirror or lens.

The only kind of curved mirrors that appear on
Physics are spherical mirrors, meaning they look like someone sliced off a piece of a sphere. Spherical mirrors have a center of curvature, represented by C in the diagram, which is the center of the sphere of which they are a slice. The radius of that sphere is called the radius of curvature, R.

All rays of light that run parallel to the principal axis will be reflected—or refracted in the case of lenses—through the same point, called the focal point, and denoted by F on the diagram. Conversely, a ray of light that passes through the focal point will be reflected parallel to the principal axis. The focal length, f, is defined as the distance between the vertex and the focal point. For spherical mirrors, the focal length is half the radius of curvature, f = R/2.

Concave Mirrors

Suppose a boy of height h stands at a distance d in front of a concave mirror. By tracing the light rays that come from the top of his head, we can see that his reflection would be at a distance d' from the mirror and it would have a height h'. As anyone who has looked into a spoon will have guessed, the image appears upside down.

The image at d' is a real image: as we can see from the ray diagram, the image is formed by actual rays of light. That means that, if you were to hold up a screen at position d', the image of the boy would be projected onto it. You may have noticed the way that the concave side of a spoon can cast light as you turn it at certain angles. That’s because concave mirrors project real images.

You’ll notice, though, that we were able to create a real image only by placing the boy behind the focal point of the mirror. What happens if he stands in front of the focal point?

The lines of the ray diagram do not converge at any point in front of the mirror, which means that no real image is formed: a concave mirror can only project real images of objects that are behind its focal point. However, we can trace the diverging lines back behind the mirror to determine the position and size of a virtual image. Like an ordinary flat mirror, the image appears to be standing behind the mirror, but no light is focused on that point behind the mirror. With mirrors generally, an image is real if it is in front of the mirror and virtual if it is behind the mirror. The virtual image is right side up, at a distance d' from the vertex, and stands at a height h'.

You can test all this yourself with the right kind of spoon. As you hold it at a distance from your face, you see your reflection upside down. As you slowly bring it closer, the upside-down reflection becomes blurred and a much larger reflection of yourself emerges, this time right side up. The image changes from upside down to right side up as your face crosses the spoon’s focal point.

Convex Mirrors

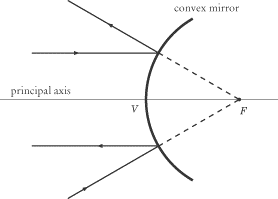
The focal point of a convex mirror is behind the mirror, so light parallel to the principal axis is reflected away from the focal point. Similarly, light moving toward the focal point is reflected parallel to the principal axis. The result is a virtual, upright image, between the mirror and the focal point.

You’ve experienced the virtual image projected by a convex mirror if you’ve ever looked into a polished doorknob. Put your face close to the knob and the image is grotesquely enlarged, but as you draw your face away, the size of the image diminishes rapidly.

The Two Equations for Mirrors and Lenses

So far we’ve talked about whether images are real or virtual, upright or upside down. We’ve also talked about images in terms of a focal length f, distances d and d', and heights h and h'. There are two formulas that relate these variables to one another, and that, when used properly, can tell whether an image is real or virtual, upright or upside down, without our having to draw any ray diagrams. These two formulas are all the math you’ll need to know for problems dealing with mirrors and lenses.

First Equation: Focal Length

The first equation relates focal length, distance of an object, and distance of an image:

Values of d, d', and f are positive if they are in front of the mirror and negative if they are behind the mirror. An object can’t be reflected unless it’s in front of a mirror, so d will always be positive. However, as we’ve seen, f is negative with convex mirrors, and d' is negative with convex mirrors and with concave mirrors where the object is closer to the mirror than the focal point. A negative value of d' signifies a virtual image, while a positive value of d' signifies a real image.

Note that a normal, flat mirror is effectively a convex mirror whose focal point is an infinite distance from the mirror, since the light rays never converge. Setting 1//f = 0, we get the expected result that the virtual image is the same distance behind the mirror as the real image is in front.

Second Equation: Magnification

The second equation tells us about the magnification, m, of an image:

The magnification tells us how large the image is with respect to the object: if 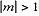, then the image is larger; if , the image is smaller; and if m = 1, as is the case in an ordinary flat mirror, the image is the same size as the object.

Because rays move in straight lines, the closer an image is to the mirror, the larger that image will appear. Note that d'/d will have a positive value with virtual images and a negative value with real images. Accordingly, the image appears upright with virtual images where m is positive, and the image appears upside down with real images where m is negative.

Example

A woman stands 40 cm from a concave mirror with a focal length of 30 cm. How far from the mirror should she set up a screen in order for her image to be projected onto it? If the woman is 1.5 m tall, how tall will her image be on the screen?

How far from the mirror should she set up a screen in order for her image to be projected onto it?

The question tells us that d = 40 cm and f = 30 cm. We can simply plug these numbers into the first of the two equations and solve for d', the distance of the image from the mirror:

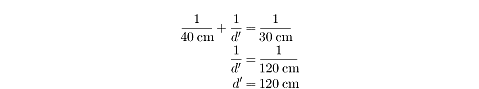
Because d' is a positive number, we know that the image will be real. Of course, we could also have inferred this from the fact that the woman sets up a screen onto which to project the image.

How tall will her image be on the screen?

We know that d = 40 cm, and we now know that d' = 120 cm, so we can plug these two values into the magnification equation and solve for m:

m = -d'/d = -120 cm/40 cm = -3

The image will be three times the height of the woman, or 1.5 × 3 = 4.5 m tall. Because the value of m is negative, we know that the image will be real, and projected upside down.

Convex Lenses

Lenses behave much like mirrors, except they use the principle of refraction, not reflection, to manipulate light. You can still apply the two equations above, but this difference between mirrors and lenses means that the values of d' and f for lenses are positive for distances behind the lens and negative for distances in front of the lens. As you might expect, d is still always positive.

Because lenses—both concave and convex—rely on refraction to focus light, the principle of dispersion tells us that there is a natural limit to how accurately the lens can focus light. For example, if you design the curvature of a convex lens so that red light is focused perfectly into the focal point, then violet light won’t be as accurately focused, since it refracts differently.

A convex lens is typically made of transparent material with a bulge in the center. Convex lenses are designed to focus light into the focal point. Because they focus light into a single point, they are sometimes called “converging” lenses. All the terminology regarding lenses is the same as the terminology we discussed with regard to mirrors—the lens has a vertex, a principal axis, a focal point, and so on.

Convex lenses differ from concave mirrors in that their focal point lies on the opposite side of the lens from the object. However, for a lens, this means that f > 0, so the two equations discussed earlier apply to both mirrors and lenses. Note also that a ray of light that passes through the vertex of a lens passes straight through without being refracted at an angle.

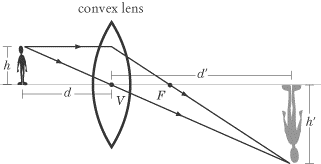
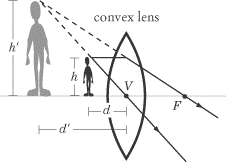
In this diagram, the boy is standing far enough from the lens that d > f. As we can see, the image is real and on the opposite side of the lens, meaning that d' is positive. Consequently, the image appears upside down, so h' and m are negative. If the boy were now to step forward so that d < f, the image would change dramatically:

Now the image is virtual and behind the boy on the same side of the lens, meaning that d' is negative. Consequently, the image appears upright, so h' and m are positive.

Concave Lenses

A concave lens is designed to divert light away from the focal point, as in the diagram. For this reason, it is often called a “diverging” lens. As with the convex lens, light passing through the vertex does not bend. Note that since the focal point F is on the same side of the lens as the object, we say the focal length f is negative.

As the diagram shows us, and as the two equations for lenses and mirrors will confirm, the image is virtual, appears on the same side of the lens as the boy does, and stands upright. This means that d' is negative and that h' and m are positive. Note that h > h', so m < 1.

Summary

There’s a lot of information to absorb about mirrors and lenses, and remembering which rules apply to which kinds of mirrors and lenses can be quite difficult. However, this information is all very systematic, so once you grasp the big picture, it’s quite easy to sort out the details. In summary, we’ll list three things that may help you grasp the big picture:

1. Learn to draw ray diagrams: Look over the diagrams of the four kinds of optical instruments and practice drawing them yourself. Remember that light refracts through lenses and reflects off mirrors. And remember that convex lenses and concave mirrors focus light to a point, while concave lenses and convex mirrors cause light to diverge away from a point.
2. Memorize the two fundamental equations: You can walk into
   Physics knowing only the two equations for lenses and mirrors and still get a perfect score on the optical instruments questions, so long as you know how to apply these equations. Remember that f is positive for concave mirrors and convex lenses, and negative for convex mirrors and concave lenses.
3. Memorize this table: Because we love you, we’ve put together a handy table that summarizes everything we’ve covered in this section of the text.

Note that when d' is positive, the image is always real and upside down, and when d' is negative, the image is always virtual and upright.

Physics questions on optical instruments are generally of two kinds. Either there will be a quantitative question that will expect you to apply one of the two equations we’ve learned, or there will be a qualitative question asking you to determine where light gets focused, whether an image is real or virtual, upright or upside down, etc.

Next to display next topic in the chapter.