Lesson: Chapter - 18

Classical Optics

Classical” optics refers to those facts about optics that were known before the adoption of the wave model of light in the nineteenth century. In Newton’s time, light was studied as if it had only particle properties—it moves in a straight line, rebounds off objects it bumps into, and passes through objects that offer minimal resistance. While this approximation of light as a particle can’t explain some of the phenomena we will look at later in this chapter, it’s perfectly adequate for dealing with most commonplace phenomena, and will serve as the basis for our examination of mirrors and lenses.

Reflection

When people think reflection, they generally think of mirrors. However, everything that we see is capable of reflecting light: if an object couldn’t reflect light, we wouldn’t be able to see it. Mirrors do present a special case, however. Most objects absorb some light, reflecting back only certain frequencies, which explains why certain objects are of certain colors. Further, most objects have a rough surface—even paper is very rough on a molecular level—and so the light reflected off them deflects in all different directions. Mirrors are so smooth that they reflect all the light that strikes them in a very predictable and convenient way.

We call the ray of light that strikes a reflective surface an incident ray, and the ray that bounces back a reflected ray. The angle of incidence, ?, is the angle between the normal—the line perpendicular to the reflective surface—and the incident ray. Similarly, the angle of reflection, ?^', is the angle between the normal and the reflected ray.

The law of reflection tells us that angle of incidence and angle of reflection are equal:

?_incidence = ?_reflection

The reflection of a ray of light works in just the same way as a ball bouncing off a wall, except gravity has no noticeable effect on light rays.

Refraction

In addition to reflecting light, many surfaces also refract light: rather than bouncing off the surface, some of the incident ray travels through the surface, but at a new angle. We are able to see through glass and water because much of the light striking these substances is refracted and passes right through them.

Light passing from one substance into another will almost always reflect partially, so there is still an incident ray and a reflected ray, and they both have the same angle to the normal. However, there is also a third ray, the refracted ray, which lies in the same plane as the incident and reflected rays. The angle of the refracted ray will not be the same as the angle of the incident and reflected rays. As a result, objects that we see in a different medium—a straw in a glass of water, for instance—appear distorted because the light bends when it passes from one medium to another.

The phenomenon of refraction results from light traveling at different speeds in different media. The “speed of light” constant c is really the speed of light in a vacuum: when light passes through matter, it slows down. If light travels through a substance with velocity v, then that substance has an index of refraction of n = c/v. Because light always travels slower through matter than through a vacuum, v is always less than or equal to c, so n = 1. For transparent materials, typical values of n are quite low: n_air = 1.0, n_water = 1.3, and n_glass = 1.6. Because it is the presence of matter that slows down light, denser materials generally have higher indices of refraction.

A light ray passing from a less dense medium into a denser medium will be refracted toward the normal, and a light ray passing from a denser medium into a less dense medium will be refracted away from the normal. For example, water is denser than air, so the light traveling out of water toward our eyes is refracted away from the normal. When we look at a straw in a glass of water, we see the straw where it would be if the light had traveled in a straight line.

Given a ray traveling from a medium with index of refraction n1 into a medium with index of refraction n2, Snell’s Law governs the relationship between the angle of incidence and the angle of refraction:

n₁ sin?₁ = n₂ sin?₂

Example

A ray of light passes from a liquid medium into a gas medium. The incident ray has an angle of 30° with the normal, and the refracted ray has an angle of 60° with the normal. If light travels through the gas at a speed of 2.5 × 10⁸ m/s, what is the speed of light through the liquid medium? sin 30° = 0.500 and sin 60° = 0.866.

We know that the index of refraction for a substance, n, gives the ratio of the speed of light in a vacuum to the speed of light in that substance. Therefore, the index of refraction, n₁, in the liquid medium is related to the speed of light, v₁, in that medium by the equation n₁ = c/v₁; similarly, the index of refraction, n₂, in the gas medium is related to the speed of light, v₂, in that medium by the equation n₂ = c/v₂. The ratio between n₁ and n₂ is:

We can calculate the ratio between n₁ and n₂ using Snell’s Law:

n₁ sin?₁ = n₂ sin?₂

n₁ (0.500) = n₂ (0.866)

n₁ / n₂ = 1.73

Since we know that the ratio of n₁ / n₂  is equal to the ration of v₂/v₁, and since we know the value for v₂, we can now calculate the value for v₁:

Given c = 3.0 × 10⁸ m/s, we can also calculate that the index of refraction for the liquid substance is 2.1, while the index of refraction for the gas substance is 1.2.

Total Internal Reflection

The sine of an angle is always a value between –1 and 1, so for certain values of n₁ , n₂, and ?₁, Snell’s Law admits no solution for ?₂. For example, suppose medium 1 is glass, medium 2 is air and ?₁ = 87°. Then the angle of refraction is given by sin?₂ = 1.6, for which there is no solution. Mathematicians have not yet invented a physical angle with this property, so physicists just shrug their shoulders and conclude that there is no refracted ray, which is supported by observation. This phenomenon is known as total internal reflection.

For two given media, the critical angle, ?_c, is defined as the smallest angle of incidence for which total internal reflection occurs. From Snell’s Law, we know that sin?₂ = n₁ sin?₁/ n₂, so refraction occurs only if n₁ sin?₁ / n₂ = 1. Setting the left side of that equation to equal 1, we can derive the critical angle:

?_c = arcsin n₁/n₂

Example

The index of refraction for water is 1.3 and the index of refraction for air is 1.0. What is the maximum angle of incidence at which a ray of light can pass from water into the air?

If the angle of incidence is greater than the critical angle, then the ray of light will not be refracted into the air. The maximum angle of incidence, then, is the critical angle.

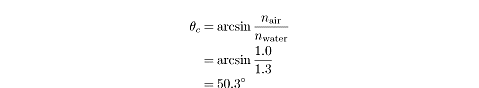
Dispersion

There is one subtlety of refraction that we’ve overlooked: the index of refraction depends slightly on the wavelength of the incident light. When a mixture of waves of different wavelength refract, each constituent color refracts differently—the different constituents disperse. Generally speaking, light of a longer wavelength and lower frequency refracts less than light of a shorter wavelength and higher frequency, so n_violet > n_red .

The phenomenon of dispersion explains why we see a rainbow when sunlight refracts off water droplets in the air. The white light of the sun is actually a mixture of a multitude of different wavelengths. When this white light passes through water droplets in the air, the different wavelengths of light are refracted differently. The violet light is refracted at a steeper angle than the red light, so the violet light that reaches our eyes appears to be coming from higher in the sky than the red light, even though they both come from the same ray of sunlight. Because each color of light is refracted at a slightly different angle, these colors arrange themselves, one on top of the other, in the sky.

We find the same phenomenon with light shone into a glass prism.

Next to display next topic in the chapter.