Lesson: Chapter - 17

Superposition

Suppose that two experimenters, holding opposite ends of a stretched string, each shake their end of the string, sending wave crests toward each other. What will happen in the middle of the string, where the two waves meet? Mathematically, you can calculate the displacement in the center by simply adding up the displacements from each of the two waves. This is called the principle of superposition: two or more waves in the same place are superimposed upon one another, meaning that they are all added together. Because of superposition, the two experimenters can each send traveling waves down the string, and each wave will arrive at the opposite end of the string undistorted by the other. The principle of superposition tells us that waves cannot affect one another: one wave cannot alter the direction, frequency, wavelength, or amplitude of another wave.

Destructive Interference

Suppose one of the experimenters yanks the string downward, while the other pulls up by exactly the same amount. In this case, the total displacement when the pulses meet will be zero: this is called destructive interference. Don’t be fooled by the name, though: neither wave is destroyed by this interference. After they pass by one another, they will continue just as they did before they met.

Constructive Interference

On the other hand, if both experimenters send upward pulses down the string, the total displacement when they meet will be a pulse that’s twice as big. This is called constructive interference.

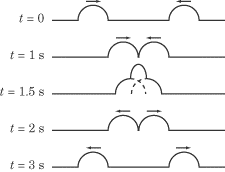
Beats

You may have noticed the phenomenon of interference when hearing two musical notes of slightly different pitch played simultaneously. You will hear a sort of “wa-wa-wa” sound, which results from repeated cycles of constructive interference, followed by destructive interference between the two waves. Each “wa” sound is called a beat, and the number of beats per second is given by the difference in frequency between the two interfering sound waves:

Example

Modern orchestras generally tune their instruments so that the note “A” sounds at 440 Hz. If one violinist is slightly out of tune, so that his “A” sounds at 438 Hz, what will be the time between the beats perceived by someone sitting in the audience?

The frequency of the beats is given by the difference in frequency between the out-of-tune violinist and the rest of the orchestra: 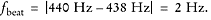Thus, there will be two beats per second, and the period for each beat will be T = 1/f = 0.5 s.

Next to display next topic in the chapter.