Lesson: Chapter - 17

Transverse Waves and Longitudinal Waves

There are two major kinds of waves: transverse waves and longitudinal waves. The medium transmitting transverse waves oscillates in a direction perpendicular to the direction the wave is traveling. A good example is waves on water: the water oscillates up and down while transmitting a wave horizontally. Other common examples include a wave on a string and electromagnetic waves. By contrast, the medium transmitting longitudinal waves oscillates in a direction parallel to the direction the wave is traveling. The most commonly discussed form of longitudinal waves is sound.

Transverse Waves: Waves on a String

Imagine—or better yet, go grab some twine and set up—a length of string stretched between two posts so that it is taut. Each point on the string is just like a mass on a spring: its equilibrium position lies on the straight line between the two posts, and if it is plucked away from its resting position, the string will exert a force to restore its equilibrium position, causing periodic oscillations. A string is more complicated than a simple mass on a spring, however, since the oscillation of each point influences nearby points along the string. Plucking a string at one end causes periodic vibrations that eventually travel down the whole length of the string. Now imagine detaching one end of the string from the pole and connecting it to a mass on a spring, which oscillates up and down, as in the figure below. The oscillation at one end of the string creates waves that propagate, or travel, down the length of the string. These are called, appropriately, traveling waves. Don’t let this name confuse you: the string itself only moves up and down, returning to its starting point once per cycle. The wave travels, but the medium—the string, in this case—only oscillates up and down.

The speed of a wave depends on the medium through which it is traveling. For a stretched string, the wave speed depends on the force of tension, F_T, exerted by the pole on the string, and on the mass density of the string, µ:

µ = total mass / total length

The formula for the wave speed is:

Example

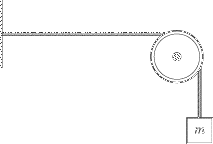
A string is tied to a pole at one end and 100 g mass at the other, and wound over a pulley. The string’s mass is 100 g, and it is 2.5 m long. If the string is plucked, at what speed do the waves travel along the string? How could you make the waves travel faster? Assume the acceleration due to gravity is 10 m/s².

Since the formula for the speed of a wave on a string is expressed in terms of the mass density of the string, we’ll need to calculate the mass density before we can calculate the wave speed.

µ = 0.1 kg / 2.5 m = 0.04 kg/m

The tension in the string is the force of gravity pulling down on the weight, F_T = mg = (0.1 kg)(10 m/s²) = 1N. The equation for calculating the speed of a wave on a string is:

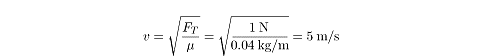
This equation suggests two ways to increase the speed of the waves: increase the tension by hanging a heavier mass from the end of the string, or replace the string with one that is less dense.

Longitudinal Waves: Sound

While waves on a string or in water are transverse, sound waves are longitudinal. The term longitudinal means that the medium transmitting the waves—air, in the case of sound waves—oscillates back and forth, parallel to the direction in which the wave is moving. This back-and-forth motion stands in contrast to the behavior of transverse waves, which oscillate up and down, perpendicular to the direction in which the wave is moving.

Imagine a slinky. If you hold one end of the slinky in each of your outstretched arms and then jerk one arm slightly toward the other, you will send a pulse across the slinky toward the other arm. This pulse is transmitted by each coil of the slinky oscillating back and forth parallel to the direction of the pulse.

When the string on a violin, the surface of a bell, or the paper cone in a stereo speaker oscillates rapidly, it creates pulses of high air pressure, or compressions, with low pressure spaces in between, called rarefactions. These compressions and rarefactions are the equivalent of crests and troughs in transverse waves: the distance between two compressions or two rarefactions is a wavelength.

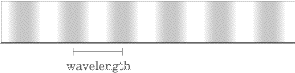
Pulses of high pressure propagate through the air much like the pulses of the slinky illustrated above, and when they reach our ears we perceive them as sound. Air acts as the medium for sound waves, just as string is the medium for waves of displacement on a string. The figure below is an approximation of sound waves in a flute—each dark area below indicates compression and represents something in the order of 10²⁴ air molecules.

Loudness, Frequency, Wavelength, and Wave Speed

Many of the concepts describing waves are related to more familiar terms describing sound. For example, the square of the amplitude of a sound wave is called its loudness, or volume. Loudness is usually measured in decibels. The decibel is a peculiar unit measured on a logarithmic scale. You won’t need to know how to calculate decibels, but it may be useful to know what they are.

The frequency of a sound wave is often called its pitch. Humans can hear sounds with frequencies as low as about 90 Hz and up to about 15,000Hz, but many animals can hear sounds with much higher frequencies. The term wavelength remains the same for sound waves. Just as in a stretched string, sound waves in air travel at a certain speed. This speed is around 343m/s under normal circumstances, but it varies with the temperature and pressure of the air. You don’t need to memorize this number: if a question involving the speed of sound comes up on the
, that quantity will be given to you.

Next to display next topic in the chapter.