Gravitational Force
In 1687, Isaac Newton published his Law of Gravitation in Philosophiae
Naturalis Principia Mathematica. Newton proposed that every body in the
universe is attracted to every other body with a force that is directly
proportional to the product of the bodies’ masses and inversely proportional to
the square of the bodies’ separation. In terms of mathematical relationships,
Newton’s Law of Gravitation states that the force of gravity,
Fg,
between two particles of mass
m1
and
m2
has a magnitude of:
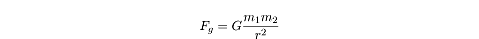
where r is the distance between the
center of the two masses and G is
the gravitational constant. The value of
G was determined experimentally by Henry Cavendish in 1798:
G = 6.67 × 10-11 N m2/kg2
The force of gravity is a vector quantity. Particle
m1
attracts particle
m2
with a force that is directed toward
m1,
as illustrated in the figure below. Similarly, particle
m2
attracts particle
m1
with a force that is directed toward
m2.
Note that the gravitational force,
Fg,
acting on particle
m1
is equal and opposite to the gravitational force acting on particle
m2,
–Fg.
This is a consequence of Newton’s Third Law.
Let’s consider two examples to give you a more intuitive feel for the strength
of the gravitational force. The force of gravity between two oranges on opposite
sides of a table is quite tiny, roughly 10–13
N. On the other hand, the gravitational force between two galaxies separated by
106 light years is something in the neighborhood of 1027 N!
Newton’s Law of Gravitation was an enormous achievement, precisely because it
synthesized the laws that govern motion on Earth and in the heavens.
Additionally, Newton’s work had a profound effect on philosophical thought. His
research implied that the universe was a rational place that could be described
by universal, scientific laws. But this is knowledge for another course. If you
are interested in learning more about it, make sure to take a class on the
history of science in college.
Gravity on the Surface of Planets
Previously, we noted that the acceleration due to gravity on Earth is
9.8 m/s2 toward the center of
the Earth. We can derive this result using Newton’s Law of Gravitation.
Consider the general case of a mass accelerating toward the center of a planet.
Applying Newton’s Second Law, we find:
Note that this equation tells us that acceleration is directly proportional to
the mass of the planet and inversely proportional to the square of the radius.
The mass of the object under the influence of the planet’s gravitational pull
doesn’t factor into the equation. This is now pretty common knowledge, but it
still trips up students on Physics: all objects under the influence of
gravity, regardless of mass, fall with the same acceleration.
Acceleration on the Surface of the Earth
To find the acceleration due to gravity on the surface of the Earth, we must
substitute values for the gravitational constant, the mass of the Earth, and the
radius of the Earth into the equation above:
Not coincidentally, this is the same number we’ve been using in all those
kinematic equations.
Acceleration Beneath the Surface of the Earth
If you were to burrow deep into the bowels of the Earth, the acceleration due to
gravity would be different. This difference would be due not only to the fact
that the value of r would have
decreased. It would also be due to the fact that not all of the Earth’s mass
would be under you. The mass above your head wouldn’t draw you toward the center
of the Earth—quite the opposite—and so the value of
would also decrease as you burrowed. It turns out that there is a linear
relationship between the acceleration due to gravity and one’s distance from the
Earth’s center when you are beneath the surface of the Earth. Burrow halfway to
the center of the Earth and the acceleration due to gravity will be
1/2 g.
Burrow three-quarters of the way to the center of the Earth and the acceleration
due to gravity will be
1 /4 g.
Orbits
The orbit of satellites—whether of artificial satellites or natural ones
like moons and planets—is a common way in which Physics will test your
knowledge of both uniform circular motion and gravitation in a single question.
How Do Orbits Work?
Imagine a baseball pitcher with a very strong arm. If he just tosses the ball
lightly, it will fall to the ground right in front of him. If he pitches the
ball at 100 miles per hour in a line
horizontal with the Earth, it will fly somewhere in the neighborhood of
80 feet before it hits the ground. By the
same token, if he were to pitch the ball at
100,000 miles per hour in a line horizontal with the Earth, it will fly
somewhere in the neighborhood of 16 miles
before it hits the ground. Now remember: the Earth is round, so if the ball
flies far enough, the ball’s downward trajectory will simply follow the
curvature of the Earth until it makes a full circle of the Earth and hits the
pitcher in the back of the head. A satellite in orbit is an object in free fall
moving at a high enough velocity that it falls around the Earth rather than back
down to the Earth.
Gravitational Force and Velocity of an Orbiting Satellite
Let’s take the example of a satellite of mass
ms
orbiting the Earth with a velocity v. The satellite is a distance
R from the center of the Earth, and
the Earth has a mass of
me.
The centripetal force acting on the satellite is the gravitational force of the
Earth. Equating the formulas for gravitational force and centripetal force we
can solve for v:
As you can see, for a planet of a given mass, each radius of orbit corresponds
with a certain velocity. That is, any object orbiting at radius
R must be orbiting with a velocity
of
.
If the satellite’s speed is too slow, then the satellite will fall back down to
Earth. If the satellite’s speed is too fast, then the satellite will fly out
into space.
div>
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.