Lesson: Chapter - 11
Gravitational Potential Energy
In Chapter 4, we learned that the potential energy of a system is equal to the
amount of work that must be done to arrange the system in that particular
configuration. We also saw that gravitational potential energy depends on
how high an object is off the ground: the higher an object is, the more work
needs to be done to get it there.
Video Lesson - Potential Energy
Gravitational potential energy is not an absolute measure. It tells us the
amount of work needed to move an object from some arbitrarily chosen reference
point to the position it is presently in. For instance, when dealing with bodies
near the surface of the Earth, we choose the ground as our reference point,
because it makes our calculations easier. If the ground is
h = 0, then for a height h above the ground an object has a potential energy of mgh.
div>
Gravitational Potential in Outer Space
Off the surface of the Earth, there’s no obvious reference point from which to
measure gravitational potential energy. Conventionally, we say that an object
that is an infinite distance away from the Earth has zero gravitational
potential energy with respect to the Earth. Because a negative amount of work is
done to bring an object closer to the Earth, gravitational potential energy is
always a negative number when using this reference point.
The gravitational potential energy of two masses,
m1
and
m2,
separated by a distance r is:
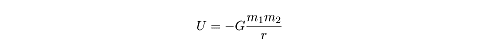
Example
|
A satellite of mass
m1
is launched from the surface of the Earth into an orbit of radius
2rc
where
rc
is the radius of the Earth. How much work is done to get it into orbit? |
The work done getting the satellite from one place to another is equal to the
change in the satellite’s potential energy. If its potential energy on the
surface of the Earth is
U1
and its potential energy when it is in orbit is
U2,
then the amount of work done is:
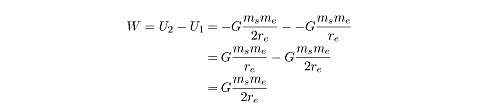
Energy of an Orbiting Satellite
Suppose a satellite of mass
ms
is in orbit around the Earth at a radius R.
We know the kinetic energy of the satellite is
KE =
1/2 mv2.
We also know that we can express centripetal force,
Fc,
as
Fc
= mv2/
class="question_inline">R. Accordingly, we can substitute this
equation into the equation for kinetic energy and get:

Because
Fc
is equal to the gravitational force, we can substitute Newton’s Law of Universal
Gravitation in for
Fc :

We know that the potential energy of the satellite is
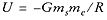 ,
so the total energy of the satellite is the sum,
E = KE + U:
,
so the total energy of the satellite is the sum,
E = KE + U:
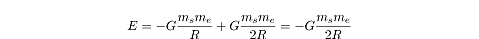
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.