Lesson: Chapter - 11
Uniform Circular Motion
Uniform circular motion occurs when a body moves in a circular path with
constant speed. For example, say you swing a tethered ball overhead in a circle:
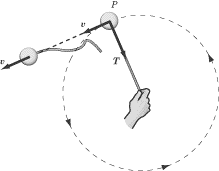
If we leave aside gravity for the moment, the only force acting on the ball is
the force of tension, T, of
the string. This force is always directed radially inward along the string,
toward your hand. In other words, the force acting on a tetherball traveling in
a circular path is always directed toward the center of that circle.
Video Lesson - Centripetal VS Centrifugal Force
Note that although the direction of the ball’s velocity changes, the ball’s
velocity is constant in magnitude and is always tangent to the circle.
Centripetal Acceleration
From kinematics, we know that acceleration is the rate of change of the velocity
vector with time. If we consider two points very close together on the ball’s
trajectory and calculate
dv,
we find that the ball’s acceleration points inward along the radius of the
circle.

The acceleration of a body experiencing uniform circular motion is always
directed toward the center of the circle, so we call that acceleration
centripetal acceleration,
ac.
Centripetal comes from a Latin word meaning “center-seeking.” We define
the centripetal acceleration of a body moving in a circle as:
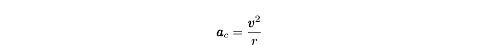
where v is the body’s
velocity, and r is the radius of the
circle. The body’s centripetal acceleration is constant in magnitude but changes
in direction. Note that even though the direction of the centripetal
acceleration vector is changing, the vector always points toward the center of
the circle.

How This Knowledge Will Be Tested
Most of us are accustomed to think of “change” as a change in magnitude, so it
may be counterintuitive to think of the acceleration vector as “changing” when
its magnitude remains constant. You’ll frequently find questions on
Physics that will try to catch you sleeping on the nature of centripetal
acceleration. These questions are generally qualitative, so if you bear in mind
that the acceleration vector is constant in magnitude, has a direction that
always points toward the center of the circle, and is always perpendicular to
the velocity vector, you should have no problem at all.
Centripetal Force
Wherever you find acceleration, you will also find force. For a body to
experience centripetal acceleration, a centripetal force must be applied
to it. The vector for this force is similar to the acceleration vector: it is of
constant magnitude, and always points radially inward to the center of the
circle, perpendicular to the velocity vector.
We can use Newton’s Second Law and the equation for centripetal acceleration to
write an equation for the centripetal force that maintains an object’s circular
motion:
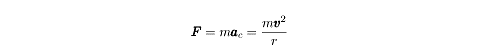
Example
|
A ball with a mass of 2 kg is swung in a circular path on a massless rope of length 0.5 m. If the ball’s speed is 1 m/s, what is the tension in the rope?
|
The tension in the rope is what provides the centripetal force, so we just need
to calculate the centripetal force using the equation above:
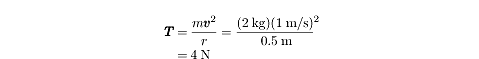
Objects Released from Circular Motion
One concept that is tested frequently on Physics is the trajectory of a
circling body when the force providing centripetal acceleration suddenly
vanishes. For example, imagine swinging a ball in a circle overhead and then
letting it go. As soon as you let go, there is no longer a centripetal force
acting on the ball. Recall Newton’s First Law: when no net force is acting on an
object, it will move with a constant velocity. When you let go of the ball, it
will travel in a straight line with the velocity it had when you let go of it.
Example
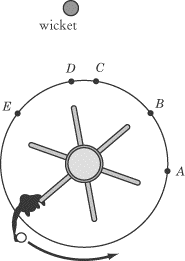
|
A student is standing on a merry-go-round that is rotating counterclockwise, as
illustrated above. The student is given a ball and told to release it in such a
way that it knocks over the wicket at the top of the diagram. At what point
should the student release the ball? |
When the student releases the ball, it will travel in a straight line, tangent
to the circle. In order to hit the wicket, then, the student should release the
ball at point B.

Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.