Torque
If a net force is applied to an object’s center of mass, it will not cause the
object to rotate. However, if a net force is applied to a point other than the
center of mass, it will affect the object’s rotation. Physicists call the effect
of force on rotational motion torque.
Video Lesson - What is Torque
Torque Defined
Consider a lever mounted on a wall so that the lever is free to move around an
axis of rotation O. In order to lift
the lever, you apply a force F
to point P, which is a distance
raway from the axis of rotation, as
illustrated below.

Suppose the lever is very heavy and resists your efforts to lift it. If you want
to put all you can into lifting this lever, what should you do? Simple intuition
would suggest, first of all, that you should lift with all your strength.
Second, you should grab onto the end of the lever, and not a point near its axis
of rotation. Third, you should lift in a direction that is perpendicular to the
lever: if you pull very hard away from the wall or push very hard toward the
wall, the lever won’t rotate at all.
Let’s summarize. In order to maximize torque, you need to:
- Maximize the magnitude of the force, F,
that you apply to the lever.
- Maximize the distance, r, from the
axis of rotation of the point on the lever to which you apply the force.
- Apply the force in a direction perpendicular to the lever.
We can apply these three requirements to an equation for torque,
 :
:

In this equation,
? is the angle made between the vector for the applied force and the lever.
Torque Defined in Terms of Perpendicular Components
There’s another way of thinking about torque that may be a bit more intuitive
than the definition provided above. Torque is the product of the distance of the
applied force from the axis of rotation and the component of the applied force
that is perpendicular to the lever arm. Or, alternatively, torque is the product
of the applied force and the component of the length of the lever arm that runs
perpendicular to the applied force.
We can express these relations mathematically as follows:
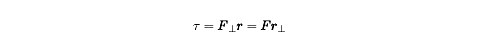
where
 and
and
 are defined below.
are defined below.
Torque Defined as a Vector Quantity
Torque, like angular velocity and angular acceleration, is a vector quantity.
Most precisely, it is the cross product of the displacement vector,
r, from the axis of rotation
to the point where the force is applied, and the vector for the applied force,
F.

To determine the direction of the torque vector, use the right-hand rule,
curling your fingers around from the r
vector over to the Fvector.
In the example of lifting the lever, the torque would be represented by a vector
at Opointing out of the page.
Example

|
|
A student exerts a force of 50 N on a lever at a distance 0.4 m from its axis of
rotation. The student pulls at an angle that is 60º above the lever arm. What
is the torque experienced by the lever arm? |
Let’s plug these values into the first equation we saw for torque:
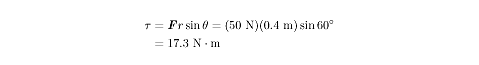
This vector has its tail at the axis of rotation, and, according to the
right-hand rule, points out of the page.
Newton’s First Law and Equilibrium
Newton’s Laws apply to torque just as they apply to force. You will find that
solving problems involving torque is made a great deal easier if you’re familiar
with how to apply Newton’s Laws to them. The First Law states:
If the net torque acting on a rigid object is zero, it will rotate with a
constant angular velocity.
The most significant application of Newton’s First Law in this context is with
regard to the concept of equilibrium. When the net torque acting on a
rigid object is zero, and that object is not already rotating, it will not begin
to rotate.
When Physics tests you on equilibrium, it will usually present you with a
system where more than one torque is acting upon an object, and will tell you
that the object is not rotating. That means that the net torque acting on the
object is zero, so that the sum of all torques acting in the clockwise direction
is equal to the sum of all torques acting in the counterclockwise direction. A
typical Physics question will ask you to determine the magnitude of one
or more forces acting on a given object that is in equilibrium.
Example
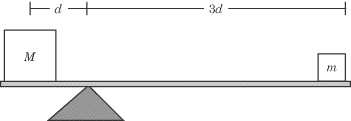
|
Two masses are balanced on the scale pictured above. If the bar connecting the two masses is horizontal and massless, what is the weight of mass m in terms of M?
|
Since the scale is not rotating, it is in equilibrium, and the net torque acting upon it must be zero. In other words, the torque exerted by mass M must be equal and opposite to the torque exerted by mass m. Mathematically,

Because mis three times as far from the axis of rotation as M, it applies three times as much torque per mass. If the two masses are to balance one another out, then M must be three times as heavy as m.
Newton’s Second Law
We have seen that acceleration has a rotational equivalent in angular acceleration, a, and that force has a rotational equivalent in torque,
 .
Just as the familiar version of Newton’s Second Law tells us that the
acceleration of a body is proportional to the force applied to it, the
rotational version of Newton’s Second Law tells us that the angular acceleration
of a body is proportional to the torque applied to it.
.
Just as the familiar version of Newton’s Second Law tells us that the
acceleration of a body is proportional to the force applied to it, the
rotational version of Newton’s Second Law tells us that the angular acceleration
of a body is proportional to the torque applied to it.
Of course, force is also proportional to mass, and there is also a rotational
equivalent for mass: the moment of inertia, I, which represents an object’s resistance to being rotated. Using the three variables,
 ,
I, and a, we can arrive at a rotational equivalent for Newton’s Second Law:
,
I, and a, we can arrive at a rotational equivalent for Newton’s Second Law:
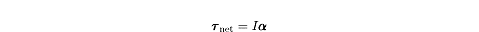
As you might have guessed, the real challenge involved in the rotational version of Newton’s Second Law is sorting out the correct value for the moment of inertia.
Moment of Inertia
What might make a body more difficult to rotate? First of all, it will be
difficult to set in a spin if it has a great mass: spinning a coin is a lot
easier than spinning a lead block. Second, experience shows that the
distribution of a body’s mass has a great effect on its potential for rotation.
In general, a body will rotate more easily if its mass is concentrated near the
axis of rotation, but the calculations that go into determining the precise
moment of inertia for different bodies is quite complex.
Moment of inertia for a single particle
Consider a particle of mass mthat is tethered by a massless string of length r
to point O, as pictured below:

The torque that produces the angular acceleration of the particle is
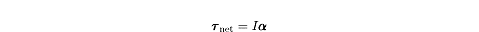 = rF, and is directed out of the
page. From the linear version of Newton’s Second Law, we know that
F = maor
F = m ar. If we multiply both sides of this
equation by r,we find:
= rF, and is directed out of the
page. From the linear version of Newton’s Second Law, we know that
F = maor
F = m ar. If we multiply both sides of this
equation by r,we find:

If we compare this equation to the rotational version of Newton’s Second Law, we
see that the moment of inertia of our particle must be
mr2.
Moment of inertia for rigid bodies
Consider a wheel, where every particle in the wheel moves around the axis of
rotation. The net torque on the wheel is the sum of the torques exerted on each
particle in the wheel. In its most general form, the rotational version of
Newton’s Second Law takes into account the moment of inertia of each individual
particle in a rotating system:
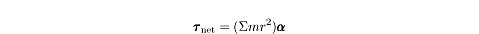
Of course, adding up the radius and mass of every particle in a system is very
tiresome unless the system consists of only two or three particles. The moment
of inertia for more complex systems can only be determined using calculus. subject test Physics doesn’t expect you to know calculus, so it will give you the moment
of inertia for a complex body whenever the need arises. For your own reference,
however, here is the moment of inertia for a few common shapes.
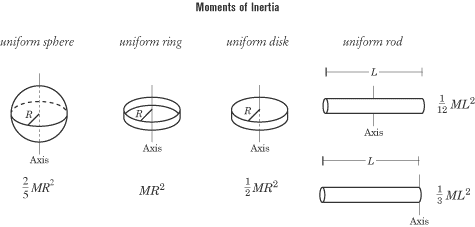
In these figures, M is the mass of
the rigid body, R is the radius of
round bodies, and Lis the distance
on a rod between the axis of rotation and the end of the rod. Note that the
moment of inertia depends on the shape and mass of the rigid body, as well as on
its axis of rotation, and that for most objects, the moment of inertia is a
multiple of MR2.
Example 1
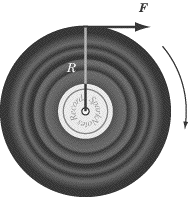
|
|
A record of mass M and radius R is free to rotate around an axis
through its center, O. A tangential force
Fis applied to the record. What must one do to maximize
the angular acceleration? |
|
|
(A) |
Make Fand M as large
as possible and R as small as possible |
|
|
(B) |
Make M as large as possible and F
and R as small as possible. |
|
|
(C) |
Make Fas large as possible
and M and R as small as possible. |
|
|
(D) |
Make R as large as possible and F
and M as small as possible. |
|
|
(E) |
Make F, M, and R
as large as possible. |
To answer this question, you don’t need to know exactly what a disc’s moment of
inertia is—you just need to be familiar with the general principle that it will
be some multiple of MR2.
The rotational version of Newton’s Second Law tells us that
 = I?,
and so
?
= FFR/I. Suppose we don’t know
what Iis, but we know that it is
some multiple of MR2.
That’s enough to formulate an equation telling us all we need to know:
= I?,
and so
?
= FFR/I. Suppose we don’t know
what Iis, but we know that it is
some multiple of MR2.
That’s enough to formulate an equation telling us all we need to know:

As we can see, the angular acceleration increases with greater force, and with
less mass and radius; therefore C is the correct answer.
Alternately, you could have answered this question by physical intuition. You
know that the more force you exert on a record, the greater its acceleration.
Additionally, if you exert a force on a small, light record, it will accelerate
faster than a large, massive record.
Example 2

|
|
The masses in the figure above are initially held at rest and are then released.
If the mass of the pulley is M, what is the angular acceleration of the
pulley? The moment of inertia of a disk spinning around its center is
1/2MR2. |
This is the only situation on Physics where you may encounter a pulley
that is not considered massless. Usually you can ignore the mass of the pulley
block, but it matters when your knowledge of rotational motion is being tested.
In order to solve this problem, we first need to determine the net torque acting
on the pulley, and then use Newton’s Second Law to determine the pulley’s
angular acceleration. The weight of each mass is transferred to the tension in
the rope, and the two forces of tension on the pulley block exert torques in
opposite directions as illustrated below:

To calculate the torque one must take into account the tension in the ropes, the
inertial resistance to motion of the hanging masses, and the inertial resistence
of the pulley itself. The sum of the torques is given by:

Solve for the tensions using Newton’s second law. For Mass 1:

For Mass 2:

Remember that a = Ra
Substitute into the first equation:
 .
.


Because
a
is positive, we know that the pulley will spin in the counterclockwise direction
and the 3m block will drop.
Next to display next topic in the chapter.
Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.