Lesson: Chapter - 8

Other Important Graphs and Equations

In addition to the graphs and equations of lines, the Math IC will test your understanding of the graphs and equations of parabolas and circles.

Questions on these topics will either ask you to match the correct graph with the correct equation or give you an equation and ask you to figure out certain characteristics of the graph.

Most of the questions about parabolas and circles are straightforward. If you know the information in the sections below, you’ll be able to breeze through them.

Parabolas

A parabola is a U-shaped curve that can open either upward or downward.

A parabola is the graph of a quadratic function, which, you may recall, is ax² + bx + c. The equation of a parabola can be expressed in two forms—the standard form and the general form. Each can help you determine different information about the nature of the parabola.

Standard Form of the Equation of a Parabola

The standard form of the equation of a parabola is perhaps the most useful and will be the one most used on the Math IC test:

where a, h, and k are constants. From this formula, you can learn a few pieces of information:

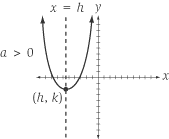
1. The vertex of the parabola is (h, k).
2. The axis of symmetry of the parabola is the line x = h.
3. The parabola opens upward if a > 0, and downward if a < 0.

For example, if you were given the parabola equation y = –3(x – 5)² + 8, you first need to pick out the values of the constants a, h, and k. Then you can derive information about the parabola. For this example, a = –3, h = 5, and k = 8. So the vertex is (5, 8), the axis of symmetry is the line x = 5, and since –3 < 0, the parabola opens downward.

General Form of the Equation of a Parabola

The general form of the equation of a parabola is:

where a, b, and c are constants. If a question presents you with a parabola equation in this form, you can find the following information about the parabola:

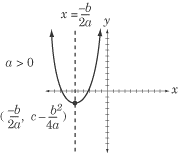
1. The vertex of the parabola is (–^b /_2a, c – ^b2/_4a).
2. The axis of symmetry of the parabola is the line x = –^b/ _2a.
3. The parabola opens upward if a > 0, and downward if a < 0.
4. The y-intercept is the point (0, c).

Circles

A circle is the collection of points equidistant from a given point, called the center of the circle. For the Math IC test, there is only one equation you have to know for a circle. This equation is called the standard form:

where (h, k) is the center of the circle, and r is the radius. When the circle is centered at the origin, so that h = k = 0, then the equation simplifies to:

That’s it. That’s all you need to know about a circle in coordinate geometry. Once you know and understand this equation, you should be able to sketch a circle in its proper place on the coordinate system if you are given its equation. You will also be asked to figure out the equation of a circle if you are given a picture of its graph.

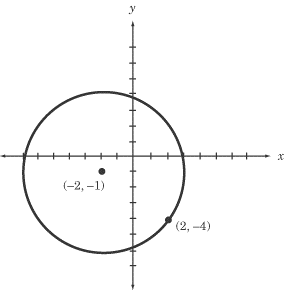
The center is given in the image: (–2, –1). All you need to finish the formula is the radius. We determine this by finding the distance from the center and the point, (2, –4), pictured on the circle:

The radius of the circle is 5, so the equation of the circle can be written as (x + 2)² + (y + 1)² = 25.

Next to display next topic in the chapter.

Mathematics Practice Questions