Lesson: Chapter - 8
Coordinate Space
When we add another dimension to the coordinate plane, creating a coordinate
space, a new axis must be introduced. Meet the z-axis:
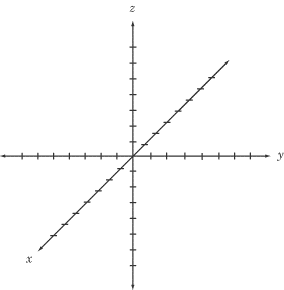
The z-axis is perpendicular to both the x- and y-axes. A
point in three dimensions is specified by three coordinates: (x, y,
z).
The only questions you’re likely to see that involve three-dimensional
coordinate geometry will ask you to calculate the distance between two points in
space. There is a general formula that allows you to make such a calculation. If
the two points are (x1, y1, z1)
and (x2, y2, z2), then the
distance between them is:
Determining the distance between two points in coordinate space is basically the
same as finding the length of the diagonal of a rectangular solid. In solid
geometry, we were given the dimensions of the sides; for coordinate geometry, we
have the coordinates of the endpoints of that diagonal.
Try the example problem below:
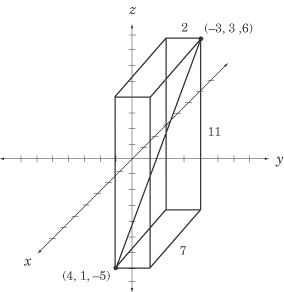
What is the distance between the points (4, 1, –5) and (–3, 3, 6)?
Using the formula, the answer is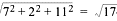
,
which approximately equals 13.19. To see this in diagram form, take a look at
the figure below:
Back
Next
Next to display next topic in the chapter.
Mathematics Practice Questions
Video Lessons and 10 Fully Explained Grand Tests
Large number of solved practice MCQ with explanations. Video Lessons and 10 Fully explained Grand/Full Tests.